Ejemplo: Interpolación spline cúbica
Utilice las funciones lspline, pspline y cspline para crear splines cúbicas (polinomios por tramos) y realizar interpolaciones entre puntos de datos.
1. Defina una matriz.
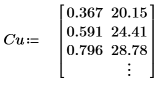
2. Utilice la función csort para ordenar los datos de modo que la segunda columna de Cu esté en orden ascendente.
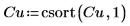
Los valores x facilitados a las funciones de spline deben estar en orden ascendente. |
3. Cree vectores que contengan los datos x e y.
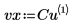
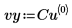
4. Utilice la función cspline para crear un vector de spline cúbico y, a continuación, utilice la función interp para obtener los valores interpolados.
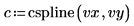
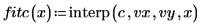
5. Utilice la función lspline para crear un vector de spline lineal y, a continuación, utilice la función interp para obtener los valores interpolados.
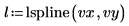
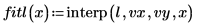
6. Utilice la función pspline para crear un vector de spline parabólico y, a continuación, utilice la función interp para obtener los valores interpolados.
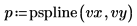
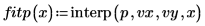
7. Trace los puntos de datos originales y las splines cúbicas.
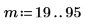
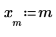
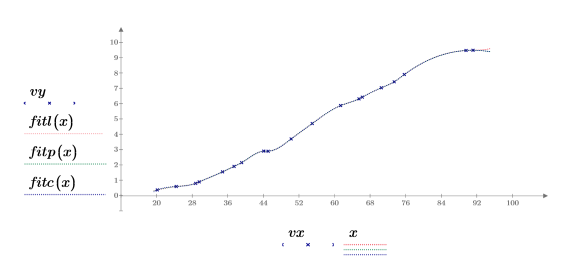
8. Amplíe los dos primeros puntos de datos.
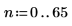
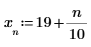
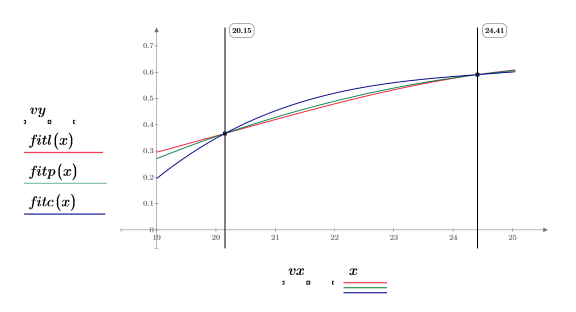
Las tres funciones de spline producen resultados equivalentes, salvo en los extremos.
9. Calcule la segunda derivada del vector de spline lineal interpolado y muestre que es igual a 0 en los puntos finales.
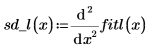 | |
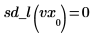 | 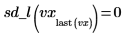 |
10. Calcule la segunda derivada del vector de spline parabólico interpolado y muestre que, en los puntos finales, es igual al valor del siguiente punto más cercano.
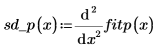
◦ Evalúe la segunda derivada en los puntos primero y segundo, y muestre que son iguales.
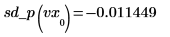
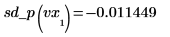
◦ Evalúe la segunda derivada en los puntos penúltimo y último, y muestre que son iguales.
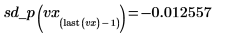
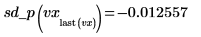
Se pueden utilizar las derivadas de los ajustes de spline para buscar los máximos y mínimos, la pendiente y otras funciones de las curvas interpoladas.