To Solve Equations Symbolically

Symbolics > Working with Symbolics > To Solve Equations Symbolically

• Type the equation to solve using the Boolean equal to operator. Insert the symbolic evaluation operator, type the keyword solve fully in the placeholder, and then press Enter or click anywhere.

<region id="ID0E14ALB" actualWidth="267.48666666666662" actualHeight="62.800000000000004" top="38.400000000000006" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="7">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <equal />
        <apply>
          <minus />
          <apply>
            <plus />
            <apply>
              <plus />
              <apply>
                <pow />
                <id xml:space="preserve">x</id>
                <real>3</real>
              </apply>
              <apply>
                <mult />
                <real>11</real>
                <apply>
                  <pow />
                  <id xml:space="preserve">x</id>
                  <real>2</real>
                </apply>
              </apply>
            </apply>
            <apply>
              <mult />
              <real>3</real>
              <id xml:space="preserve">x</id>
            </apply>
          </apply>
          <real>135</real>
        </apply>
        <real>0</real>
      </apply>
      <command>
        <id xml:space="preserve">solve</id>
      </command>
      <symResult>
        <matrix rows="3" cols="1">
          <real>3</real>
          <real>-5</real>
          <real>-9</real>
        </matrix>
      </symResult>
    </symEval>
  </math>
</region>

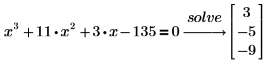
If you type the keyword solve instead of solve fully, the returned solution may be partial, only in numeric form, or a math expression without domain details. Typing the keyword solve fully returns all solutions, including refinement of domain and conditions for formula variables. For example: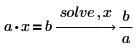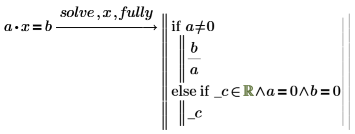

PTC Mathcad returns symbolic solutions to the equation, if possible. Otherwise, it returns numeric solutions. If the equation you are trying to solve has more than one solution, PTC Mathcad returns the solutions in a vector, unless the solution is periodic.

• To solve an equation whose right-hand side is set to 0, you only need to type the left-hand side of the equation.

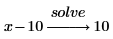
• If the equation contains more than one variable, specify a comma-separated list of variables you want to solve for after solve.

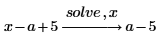
• If your equation includes numbers with decimal points, solve returns a decimal answer.

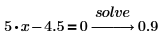
• To solve an equation subject to restrictions on the domain of the variable, for example, solving over the real numbers, use the keyword assume and a modifier with solve.

<region id="ID0EAHBLB" actualWidth="361.00933364629748" actualHeight="75.29066705465317" top="307.20000000000005" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="11">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <equal />
        <apply>
          <mult />
          <parens>
            <apply>
              <minus />
              <apply>
                <pow />
                <id xml:space="preserve">x</id>
                <real>3</real>
              </apply>
              <real>1</real>
            </apply>
          </parens>
          <parens>
            <apply>
              <minus />
              <apply>
                <pow />
                <id xml:space="preserve">x</id>
                <real>2</real>
              </apply>
              <real>2</real>
            </apply>
          </parens>
        </apply>
        <real>0</real>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">solve</id>
            <id xml:space="preserve">assume</id>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">x</id>
            <id xml:space="preserve">real</id>
          </apply>
        </sequence>
      </command>
      <symResult>
        <matrix rows="3" cols="1">
          <apply>
            <nthRoot />
            <placeholder />
            <real>2</real>
          </apply>
          <apply>
            <neg />
            <apply>
              <nthRoot />
              <placeholder />
              <real>2</real>
            </apply>
          </apply>
          <real>1</real>
        </matrix>
      </symResult>
    </symEval>
  </math>
</region>

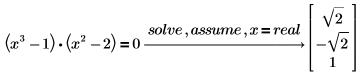
• If an equation has a periodic solution, solve returns a single value from the set of solutions.

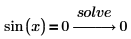
To see a more detailed solution, add the modifier fully after solve.

<region id="ID0EPJBLB" actualWidth="275.65666666666669" actualHeight="112" top="480.00000000000006" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="13">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <equal />
        <apply>
          <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">sin</id>
          <id xml:space="preserve">x</id>
        </apply>
        <real>0</real>
      </apply>
      <command>
        <sequence>
          <id xml:space="preserve">solve</id>
          <id xml:space="preserve">fully</id>
        </sequence>
      </command>
      <symResult>
        <program>
          <if>
            <test>
              <apply>
                <elementOf />
                <id xml:space="preserve" labels="*">_n</id>
                <id xml:space="preserve" labels="CONSTANT">ℤ</id>
              </apply>
            </test>
            <then>
              <program>
                <apply>
                  <mult />
                  <id xml:space="preserve" labels="*">_n</id>
                  <id xml:space="preserve" labels="CONSTANT">π</id>
                </apply>
              </program>
            </then>
            <else>
              <program>
                <id xml:space="preserve" labels="*">undefined</id>
              </program>
            </else>
          </if>
        </program>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

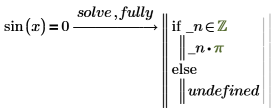
• PTC Mathcad returns the solution in terms of a newly generated variable that represents an arbitrary integer. The generated variable is preceded by an underscore to avoid conflicts with other variables you may have defined elsewhere in the worksheet.

• To solve a system of equations symbolically, you can create a column vector with each element holding one equation in the system. Then solve using the symbolics operator, specifying a column vector or a comma-separated list of system variables after the solve keyword.

◦ To solve an inequality, use >, <, ≤ , or ≥ in place of =.

◦ You can include constraint equations in a column vector to restrict the solution to a range, for example, y > 0.

◦ Solving systems of equations, inequality equations, or periodic equations may produce some special results that do not have meaning when evaluated numerically.

◦ You can find roots numerically using the root function, solve linear systems numerically using the lsolve function, or solve linear or nonlinear systems using a solve block.