To Evaluate Integrals Symbolically

Symbolics > Working with Symbolics > Calculus > To Evaluate Integrals Symbolically

To Evaluate Integrals Symbolically

1. Insert the integral operator.

2. Type the expression in the placeholder to the right of the integral sign.

3. Type the integration variable x in the placeholder to the right of the symbol d.

4. Insert the symbolic evaluation operator.

<region id="ID0EZPHLB" actualWidth="221.93666666666667" actualHeight="58.952000000000005" top="19.200000000000003" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="6">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">x</id>
          </boundVars>
          <apply>
            <mult />
            <apply>
              <pow />
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
              <real>2</real>
            </apply>
            <apply>
              <pow />
              <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">e</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <placeholder />
        </lowerBound>
        <upperBound>
          <placeholder />
        </upperBound>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <mult />
          <parens>
            <apply>
              <plus />
              <apply>
                <minus />
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="VARIABLE">x</id>
                  <real>2</real>
                </apply>
                <apply>
                  <mult />
                  <real>2</real>
                  <id xml:space="preserve" labels="VARIABLE">x</id>
                </apply>
              </apply>
              <real>2</real>
            </apply>
          </parens>
          <apply>
            <pow />
            <id xml:space="preserve" labels="CONSTANT">e</id>
            <id xml:space="preserve" labels="VARIABLE">x</id>
          </apply>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

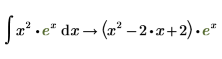
You can only evaluate the indefinite integral using the symbolic evaluation operator.

5. To take the definite integral of the same function, from 0 through 5, type 0 in the bottom placeholder of the integral. Type 5 in the top placeholder, and repeat steps 2-4.

<region id="ID0EDSHLB" actualWidth="168.5266666666667" actualHeight="58.952000000000005" top="96.000000000000014" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="7">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">x</id>
          </boundVars>
          <apply>
            <mult />
            <apply>
              <pow />
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
              <real>2</real>
            </apply>
            <apply>
              <pow />
              <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">e</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <real>5</real>
        </upperBound>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <minus />
          <apply>
            <mult />
            <real>17</real>
            <apply>
              <pow />
              <id xml:space="preserve" labels="CONSTANT">e</id>
              <real>5</real>
            </apply>
          </apply>
          <real>2</real>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

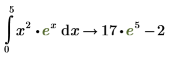
Cauchy Principal Value

The Cauchy principal value of the integral about a point c, in the interval (a,b), is defined by the following expression:

<region id="ID0EWTHLB" actualWidth="213.65666666666669" actualHeight="58.800000000000004" top="230.40000000000003" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="9">
    <apply xmlns="http://schemas.mathsoft.com/math50">
      <limit direction="right" />
      <lambda>
        <boundVars>
          <id xml:space="preserve">ε</id>
        </boundVars>
        <parens>
          <apply>
            <plus />
            <apply>
              <integral />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <apply>
                  <id xml:space="preserve">f</id>
                  <id xml:space="preserve">x</id>
                </apply>
              </lambda>
              <lowerBound>
                <id xml:space="preserve">a</id>
              </lowerBound>
              <upperBound>
                <apply>
                  <minus />
                  <id xml:space="preserve">c</id>
                  <id xml:space="preserve">ε</id>
                </apply>
              </upperBound>
            </apply>
            <apply>
              <integral />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">x</id>
                </boundVars>
                <apply>
                  <id xml:space="preserve">f</id>
                  <id xml:space="preserve">x</id>
                </apply>
              </lambda>
              <lowerBound>
                <apply>
                  <plus />
                  <id xml:space="preserve">c</id>
                  <id xml:space="preserve">ε</id>
                </apply>
              </lowerBound>
              <upperBound>
                <id xml:space="preserve">b</id>
              </upperBound>
            </apply>
          </apply>
        </parens>
      </lambda>
      <real>0</real>
    </apply>
  </math>
</region>

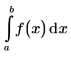
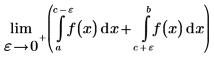
The purpose of the Cauchy principal value is to define the value of the integral when the function f has a singularity point at c. For example, the following integral has a singularity point at c=0, and the symbolic evaluation returns an error.

Click to copy this expression

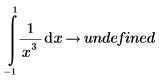
To find the Cauchy principal value of the integral, add the modifier cauchy.

Click to copy this expression

<region id="ID0EMVHLB" actualWidth="137.65333333333334" actualHeight="80.552" top="403.2000000000001" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="11">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">x</id>
          </boundVars>
          <apply>
            <div />
            <real>1</real>
            <apply>
              <pow />
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
              <real>3</real>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <real>-1</real>
        </lowerBound>
        <upperBound>
          <real>1</real>
        </upperBound>
      </apply>
      <command>
        <id xml:space="preserve">cauchy</id>
      </command>
      <symResult>
        <real>0</real>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

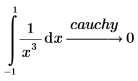
Symbolic evaluation of integrals that require Cauchy analysis return a result of undefined unless the cauchy keyword is specified.

Related Topics

About Symbolic Calculus

To Evaluate Derivatives Symbolically

Cauchy Distribution

Example: Symbolic Calculus I

Example: Symbolic Calculus II

Was this helpful?