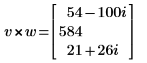Example: Vector Algebra
1. Define a vector and view its simplified form.
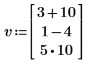
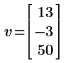
2. Add a complex vector to v.
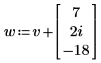
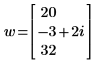
3. Find the negative of vector w.
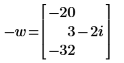
4. Multiply vector w by a scalar.
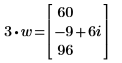
5. Sum the components of vector v. Press Ctrl+Shift+$ to insert the summation operator.
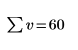
This is equivalent to the following calculation: 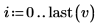 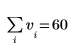 |
6. Find the magnitude of vector w. Press Ctrl+Shift+| to insert the Norm operator.
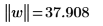
This is equivalent to the following calculation: 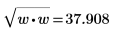 |
7. Transpose vector w. Press Ctrl+Shift+T to insert the transpose operator.
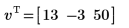
8. Find the complex conjugate of vector w. Press Ctrl+Shift+_ to insert the complex conjugate operator.
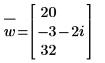
9. Calculate the dot product of vectors v and w.
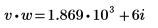
The dot product is calculated by multiplying each element of the first vector by the corresponding element of the complex conjugate of the second vector, and then summing the result.
10. Calculate the cross product of vectors v and w. Press Ctrl+8 to insert the cross product operator.