Example: Symbolic Elliptic Integral Functions

Symbolics > Working with Symbolics > Calculus > Example: Symbolic Elliptic Integral Functions

The following elliptic integral functions appear in many symbolic calculations.

The elliptic integral functions are not part of the PTC Mathcad Prime set of built-in functions.

EllipticK: The Complete Elliptic Integral of the First Kind

1. Show the definition of the complete elliptic integral of the first kind, EllipticK(m).

<region id="ID0EM5SLB" actualWidth="293.58533395926162" actualHeight="85.8289335273266" top="230.40000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="34">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">EllipticK</id>
        <boundVars>
          <id labels="*" xml:space="preserve">m</id>
        </boundVars>
      </function>
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">τ</id>
          </boundVars>
          <apply>
            <div />
            <real>1</real>
            <apply>
              <mult />
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <minus />
                  <real>1</real>
                  <apply>
                    <pow />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                    <real>2</real>
                  </apply>
                </apply>
              </apply>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <minus />
                  <real>1</real>
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                    <apply>
                      <pow />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                      <real>2</real>
                    </apply>
                  </apply>
                </apply>
              </apply>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <real>1</real>
        </upperBound>
      </apply>
    </define>
  </math>
</region>

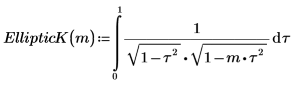
2. Evaluate EllipticK numerically.

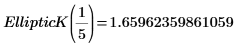
3. Plot the numerical values of EllipticK in the range of 0<m<1.

<region id="ID0EDDTLB" actualWidth="39.22" actualHeight="25.6" top="422.40000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="36"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">s</id> <real>0</real> </define> </math> </region>	<region id="ID0EXDTLB" actualWidth="77.77000000000001" actualHeight="25.6" top="422.40000000000009" left="115.20000000000002" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="37"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">d</id> <real>0.0025</real> </define> </math> </region>	<region id="ID0ELETLB" actualWidth="73.81" actualHeight="25.6" top="422.40000000000009" left="211.20000000000005" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="38"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">l</id> <real>9.9975</real> </define> </math> </region>
<region id="ID0EFFTLB" actualWidth="71.876666666666665" actualHeight="25.6" top="422.40000000000009" left="326.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="39"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">u</id> <range> <sequence> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">s</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">d</id> </sequence> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">l</id> </range> </define> </math> </region>
<region id="ID0EOGTLB" actualWidth="164.44666666666669" actualHeight="36.800000000000004" top="480.00000000000006" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="40"> <define xmlns="http://schemas.mathsoft.com/math50"> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve">EK0</id> <apply> <scale /> <real>400</real> <id labels="*" xml:space="preserve">u</id> </apply> </apply> <apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EllipticK</id> <real>0</real> </apply> </define> </math> </region>	<region id="ID0ECHTLB" actualWidth="177.3" actualHeight="47.2" top="480.00000000000006" left="268.80000000000007" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="41"> <define xmlns="http://schemas.mathsoft.com/math50"> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve">EK1</id> <apply> <scale /> <real>400</real> <id labels="*" xml:space="preserve">u</id> </apply> </apply> <apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EllipticK</id> <apply> <div /> <id xml:space="preserve">u</id> <real>10</real> </apply> </apply> </define> </math> </region>
<region id="ID0EBITLB" actualWidth="177.3" actualHeight="47.2" top="537.60000000000014" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="42"> <define xmlns="http://schemas.mathsoft.com/math50"> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve">EK2</id> <apply> <scale /> <real>400</real> <id labels="*" xml:space="preserve">u</id> </apply> </apply> <apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EllipticK</id> <apply> <div /> <id xml:space="preserve">u</id> <real>15</real> </apply> </apply> </define> </math> </region>	<region id="ID0EVITLB" actualWidth="177.3" actualHeight="47.2" top="537.60000000000014" left="268.80000000000007" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="43"> <define xmlns="http://schemas.mathsoft.com/math50"> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve">EK3</id> <apply> <scale /> <real>400</real> <id labels="*" xml:space="preserve">u</id> </apply> </apply> <apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EllipticK</id> <apply> <div /> <id xml:space="preserve">u</id> <real>30</real> </apply> </apply> </define> </math> </region>

<region id="ID0EOJTLB" actualWidth="576.8" actualHeight="307.20000000000005" top="576.00000000000011" left="38.400000000000006" height="307.20000000000005" width="576.8" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="44">
          <traceStyle color="#FF662D91" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="45">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
        <trace resultRef="46">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
        <trace resultRef="47">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="442.4" height="230.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="10">
          <axisLine position="bottom" positionticmark="-1" legendWidth="61.21" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="1" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">u</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="1.5" end="5.9">
          <axisLine position="origin" positionticmark="0" legendWidth="106.56" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="48" display="true" color="#FF000000" line-style="Dash" value="5.53360271249443">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <id xml:space="preserve">EllipticK</id>
                <apply>
                  <div />
                  <id xml:space="preserve">l</id>
                  <real>10</real>
                </apply>
              </apply>
            </marker>
          </markers>
          <numberFormat>
            <general precision="1" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EK0</id>
                  <real>400</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EK1</id>
                  <apply>
                    <scale />
                    <real>400</real>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">u</id>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EK2</id>
                  <apply>
                    <scale />
                    <real>400</real>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">u</id>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EK3</id>
                  <apply>
                    <scale />
                    <real>400</real>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">u</id>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="49">
              <real xmlns="http://schemas.mathsoft.com/math50">1.5</real>
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

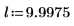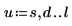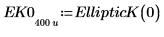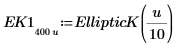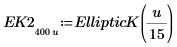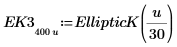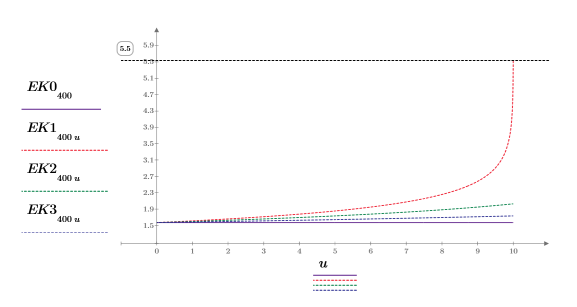
The integral equals π/2 when m=0, and approaches 12 as m approaches 1. The horizontal marker shows the value of Elliptick(l/10), or:

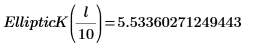
EllipticF: The Incomplete Elliptic Integral of the First Kind

1. Show the definition of the incomplete elliptic integral of the first kind, EllipticF(x, m).

<region id="ID0EWMTLB" actualWidth="315.16700062592827" actualHeight="85.8289335273266" top="1152.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="51">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">EllipticF</id>
        <boundVars>
          <id labels="*" xml:space="preserve">x</id>
          <id labels="*" xml:space="preserve">m</id>
        </boundVars>
      </function>
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">τ</id>
          </boundVars>
          <apply>
            <div />
            <real>1</real>
            <apply>
              <mult />
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <minus />
                  <real>1</real>
                  <apply>
                    <pow />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                    <real>2</real>
                  </apply>
                </apply>
              </apply>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <minus />
                  <real>1</real>
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                    <apply>
                      <pow />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                      <real>2</real>
                    </apply>
                  </apply>
                </apply>
              </apply>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <apply>
            <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">sin</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
          </apply>
        </upperBound>
      </apply>
    </define>
  </math>
</region>

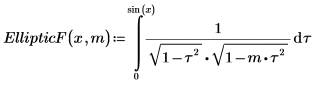
2. Evaluate EllipticF numerically.

<region id="ID0EKOTLB" actualWidth="268.98" actualHeight="47.2" top="1286.4" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="52">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EllipticF</id>
        <sequence>
          <apply>
            <div />
            <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id>
            <real>2</real>
          </apply>
          <apply>
            <div />
            <real>1</real>
            <real>5</real>
          </apply>
        </sequence>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
    <resultFormat>
      <general precision="15" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="1,1" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

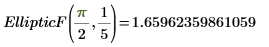
3. Show the relationship between EllipticF and EllipticK.

<region id="ID0ECQTLB" actualWidth="354.59533395926167" actualHeight="85.8289335273266" top="1401.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="53">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EllipticF</id>
        <sequence>
          <apply>
            <div />
            <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id>
            <real>2</real>
          </apply>
          <id xml:space="preserve">m</id>
        </sequence>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <integral />
          <lambda>
            <boundVars>
              <id labels="VARIABLE" xml:space="preserve">τ</id>
            </boundVars>
            <apply>
              <div />
              <real>1</real>
              <apply>
                <mult />
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <plus />
                    <apply>
                      <neg />
                      <parens>
                        <apply>
                          <mult />
                          <apply>
                            <pow />
                            <id labels="VARIABLE" xml:space="preserve">τ</id>
                            <real>2</real>
                          </apply>
                          <id labels="*" xml:space="preserve">m</id>
                        </apply>
                      </parens>
                    </apply>
                    <real>1</real>
                  </apply>
                </apply>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <plus />
                    <apply>
                      <neg />
                      <apply>
                        <pow />
                        <id labels="VARIABLE" xml:space="preserve">τ</id>
                        <real>2</real>
                      </apply>
                    </apply>
                    <real>1</real>
                  </apply>
                </apply>
              </apply>
            </apply>
          </lambda>
          <lowerBound>
            <real>0</real>
          </lowerBound>
          <upperBound>
            <real>1</real>
          </upperBound>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

<region id="ID0EQQTLB" actualWidth="332.27200062592829" actualHeight="85.8289335273266" top="1401.6000000000001" left="441.60000000000008" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="54">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EllipticK</id>
        <id xml:space="preserve">m</id>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <integral />
          <lambda>
            <boundVars>
              <id labels="VARIABLE" xml:space="preserve">τ</id>
            </boundVars>
            <apply>
              <div />
              <real>1</real>
              <apply>
                <mult />
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <plus />
                    <apply>
                      <neg />
                      <parens>
                        <apply>
                          <mult />
                          <apply>
                            <pow />
                            <id labels="VARIABLE" xml:space="preserve">τ</id>
                            <real>2</real>
                          </apply>
                          <id labels="*" xml:space="preserve">m</id>
                        </apply>
                      </parens>
                    </apply>
                    <real>1</real>
                  </apply>
                </apply>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <plus />
                    <apply>
                      <neg />
                      <apply>
                        <pow />
                        <id labels="VARIABLE" xml:space="preserve">τ</id>
                        <real>2</real>
                      </apply>
                    </apply>
                    <real>1</real>
                  </apply>
                </apply>
              </apply>
            </apply>
          </lambda>
          <lowerBound>
            <real>0</real>
          </lowerBound>
          <upperBound>
            <real>1</real>
          </upperBound>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

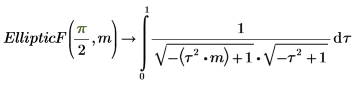
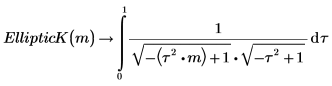
The two integrals are equal.

EllipticE: The Elliptic Integral of the Second Kind

1. Show the definition of the complete elliptic integral of the second kind, EllipticE(m):

<region id="ID0EVSTLB" actualWidth="229.69600031296412" actualHeight="93.257867054653175" top="1632.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="55">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="VARIABLE" xml:space="preserve">EllipticE</id>
        <boundVars>
          <id labels="VARIABLE" xml:space="preserve">m</id>
        </boundVars>
      </function>
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">τ</id>
          </boundVars>
          <apply>
            <div />
            <apply>
              <nthRoot />
              <placeholder />
              <apply>
                <minus />
                <real>1</real>
                <apply>
                  <mult />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                  <apply>
                    <pow />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                    <real>2</real>
                  </apply>
                </apply>
              </apply>
            </apply>
            <apply>
              <nthRoot />
              <placeholder />
              <apply>
                <minus />
                <real>1</real>
                <apply>
                  <pow />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                  <real>2</real>
                </apply>
              </apply>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <real>1</real>
        </upperBound>
      </apply>
    </define>
  </math>
</region>

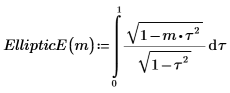
Alternatively, the function is given by:

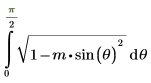
2. Evaluate EllipticE numerically.

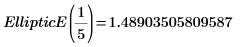
3. Show the definition of the incomplete elliptic integral of the second kind, EllipticE(x, m):

<region id="ID0EPWTLB" actualWidth="257.76100031296414" actualHeight="93.257867054653175" top="2016.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="58">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="VARIABLE" xml:space="preserve">EllipticEi</id>
        <boundVars>
          <id labels="VARIABLE" xml:space="preserve">x</id>
          <id labels="VARIABLE" xml:space="preserve">m</id>
        </boundVars>
      </function>
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">τ</id>
          </boundVars>
          <apply>
            <div />
            <apply>
              <nthRoot />
              <placeholder />
              <apply>
                <minus />
                <real>1</real>
                <apply>
                  <mult />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                  <apply>
                    <pow />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                    <real>2</real>
                  </apply>
                </apply>
              </apply>
            </apply>
            <apply>
              <nthRoot />
              <placeholder />
              <apply>
                <minus />
                <real>1</real>
                <apply>
                  <pow />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                  <real>2</real>
                </apply>
              </apply>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <apply>
            <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">sin</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
          </apply>
        </upperBound>
      </apply>
    </define>
  </math>
</region>

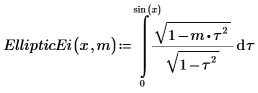
4. Evaluate EllipticEi numerically.

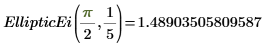
5. Show the relationship between EllipticE and EllipticEi.

<region id="ID0E2ZTLB" actualWidth="341.93933364629743" actualHeight="83.10266633224488" top="2246.4000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="60">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EllipticE</id>
        <id xml:space="preserve">m</id>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <integral />
          <lambda>
            <boundVars>
              <id labels="VARIABLE" xml:space="preserve">τ</id>
            </boundVars>
            <apply>
              <mult />
              <apply>
                <pow />
                <parens>
                  <apply>
                    <plus />
                    <apply>
                      <neg />
                      <apply>
                        <pow />
                        <id labels="VARIABLE" xml:space="preserve">τ</id>
                        <real>2</real>
                      </apply>
                    </apply>
                    <real>1</real>
                  </apply>
                </parens>
                <apply>
                  <neg />
                  <apply>
                    <div />
                    <real>1</real>
                    <real>2</real>
                  </apply>
                </apply>
              </apply>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <plus />
                  <apply>
                    <neg />
                    <parens>
                      <apply>
                        <mult />
                        <apply>
                          <pow />
                          <id labels="VARIABLE" xml:space="preserve">τ</id>
                          <real>2</real>
                        </apply>
                        <id labels="*" xml:space="preserve">m</id>
                      </apply>
                    </parens>
                  </apply>
                  <real>1</real>
                </apply>
              </apply>
            </apply>
          </lambda>
          <lowerBound>
            <real>0</real>
          </lowerBound>
          <upperBound>
            <real>1</real>
          </upperBound>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

<region id="ID0EJ1TLB" actualWidth="370.74600031296416" actualHeight="83.10266633224488" top="2342.4000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="61">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EllipticEi</id>
        <sequence>
          <apply>
            <div />
            <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id>
            <real>2</real>
          </apply>
          <id xml:space="preserve">m</id>
        </sequence>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <integral />
          <lambda>
            <boundVars>
              <id labels="VARIABLE" xml:space="preserve">τ</id>
            </boundVars>
            <apply>
              <mult />
              <apply>
                <pow />
                <parens>
                  <apply>
                    <plus />
                    <apply>
                      <neg />
                      <apply>
                        <pow />
                        <id labels="VARIABLE" xml:space="preserve">τ</id>
                        <real>2</real>
                      </apply>
                    </apply>
                    <real>1</real>
                  </apply>
                </parens>
                <apply>
                  <neg />
                  <apply>
                    <div />
                    <real>1</real>
                    <real>2</real>
                  </apply>
                </apply>
              </apply>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <plus />
                  <apply>
                    <neg />
                    <parens>
                      <apply>
                        <mult />
                        <apply>
                          <pow />
                          <id labels="VARIABLE" xml:space="preserve">τ</id>
                          <real>2</real>
                        </apply>
                        <id labels="*" xml:space="preserve">m</id>
                      </apply>
                    </parens>
                  </apply>
                  <real>1</real>
                </apply>
              </apply>
            </apply>
          </lambda>
          <lowerBound>
            <real>0</real>
          </lowerBound>
          <upperBound>
            <real>1</real>
          </upperBound>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

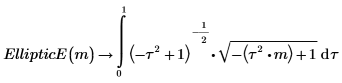
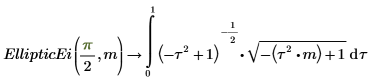
The two integrals are equal.

EllipticP: The Elliptic Integral of the Third Kind

1. Show the definition of the complete elliptic integral of the third kind, EllipticPi(n, m):

<region id="ID0EO3TLB" actualWidth="388.668667292595" actualHeight="85.8289335273266" top="2534.4000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="62">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="VARIABLE" xml:space="preserve">EllipticP</id>
        <boundVars>
          <id labels="VARIABLE" xml:space="preserve">n</id>
          <id labels="VARIABLE" xml:space="preserve">m</id>
        </boundVars>
      </function>
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">τ</id>
          </boundVars>
          <apply>
            <div />
            <real>1</real>
            <apply>
              <mult />
              <apply>
                <mult />
                <parens>
                  <apply>
                    <minus />
                    <real>1</real>
                    <apply>
                      <mult />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id>
                      <apply>
                        <pow />
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                        <real>2</real>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <minus />
                    <real>1</real>
                    <apply>
                      <pow />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                      <real>2</real>
                    </apply>
                  </apply>
                </apply>
              </apply>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <minus />
                  <real>1</real>
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                    <apply>
                      <pow />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                      <real>2</real>
                    </apply>
                  </apply>
                </apply>
              </apply>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <real>1</real>
        </upperBound>
      </apply>
    </define>
  </math>
</region>

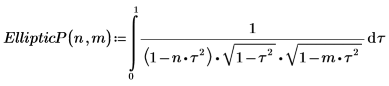
2. Evaluate EllipticP(n, m) numerically.

<region id="ID0EC5TLB" actualWidth="229.12333333333333" actualHeight="47.2" top="2668.8" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="63">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EllipticP</id>
        <sequence>
          <apply>
            <div />
            <id labels="CONSTANT" xml:space="preserve">π</id>
            <real>4</real>
          </apply>
          <apply>
            <div />
            <real>1</real>
            <real>5</real>
          </apply>
        </sequence>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
    <resultFormat>
      <general precision="9" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="1,1" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

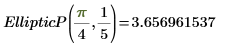
3. Show the definition of the incomplete elliptic integral of the third kind, EllipticPi(x, n, m):

<region id="ID0EW6TLB" actualWidth="416.73366729259493" actualHeight="85.8289335273266" top="2784.0000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="64">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="VARIABLE" xml:space="preserve">EllipticPi</id>
        <boundVars>
          <id labels="VARIABLE" xml:space="preserve">x</id>
          <id labels="VARIABLE" xml:space="preserve">n</id>
          <id labels="VARIABLE" xml:space="preserve">m</id>
        </boundVars>
      </function>
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">τ</id>
          </boundVars>
          <apply>
            <div />
            <real>1</real>
            <apply>
              <mult />
              <apply>
                <mult />
                <parens>
                  <apply>
                    <minus />
                    <real>1</real>
                    <apply>
                      <mult />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id>
                      <apply>
                        <pow />
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                        <real>2</real>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <minus />
                    <real>1</real>
                    <apply>
                      <pow />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                      <real>2</real>
                    </apply>
                  </apply>
                </apply>
              </apply>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <minus />
                  <real>1</real>
                  <apply>
                    <mult />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                    <apply>
                      <pow />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">τ</id>
                      <real>2</real>
                    </apply>
                  </apply>
                </apply>
              </apply>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <apply>
            <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">sin</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
          </apply>
        </upperBound>
      </apply>
    </define>
  </math>
</region>

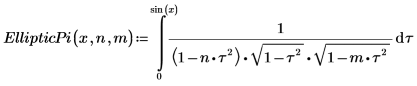
4. Evaluate EllipticPi numerically.

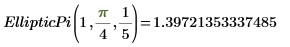
5. Show the relationship between EllipticP and EllipticPi.

<region id="ID0ECDULB" actualWidth="438.10533395926154" actualHeight="85.8289335273266" top="3033.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="66">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EllipticP</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id>
          <id xml:space="preserve">m</id>
        </sequence>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <integral />
          <lambda>
            <boundVars>
              <id labels="VARIABLE" xml:space="preserve">τ</id>
            </boundVars>
            <apply>
              <neg />
              <apply>
                <div />
                <real>1</real>
                <apply>
                  <mult />
                  <apply>
                    <mult />
                    <parens>
                      <apply>
                        <minus />
                        <apply>
                          <mult />
                          <apply>
                            <pow />
                            <id labels="VARIABLE" xml:space="preserve">τ</id>
                            <real>2</real>
                          </apply>
                          <id labels="*" xml:space="preserve">n</id>
                        </apply>
                        <real>1</real>
                      </apply>
                    </parens>
                    <apply>
                      <nthRoot />
                      <placeholder />
                      <apply>
                        <plus />
                        <apply>
                          <neg />
                          <parens>
                            <apply>
                              <mult />
                              <apply>
                                <pow />
                                <id labels="VARIABLE" xml:space="preserve">τ</id>
                                <real>2</real>
                              </apply>
                              <id labels="*" xml:space="preserve">m</id>
                            </apply>
                          </parens>
                        </apply>
                        <real>1</real>
                      </apply>
                    </apply>
                  </apply>
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <apply>
                      <plus />
                      <apply>
                        <neg />
                        <apply>
                          <pow />
                          <id labels="VARIABLE" xml:space="preserve">τ</id>
                          <real>2</real>
                        </apply>
                      </apply>
                      <real>1</real>
                    </apply>
                  </apply>
                </apply>
              </apply>
            </apply>
          </lambda>
          <lowerBound>
            <real>0</real>
          </lowerBound>
          <upperBound>
            <real>1</real>
          </upperBound>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

<region id="ID0EQDULB" actualWidth="466.1703339592616" actualHeight="85.8289335273266" top="3129.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="67">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">EllipticPi</id>
        <sequence>
          <id xml:space="preserve">x</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id>
          <id xml:space="preserve">m</id>
        </sequence>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <integral />
          <lambda>
            <boundVars>
              <id labels="VARIABLE" xml:space="preserve">τ</id>
            </boundVars>
            <apply>
              <neg />
              <apply>
                <div />
                <real>1</real>
                <apply>
                  <mult />
                  <apply>
                    <mult />
                    <parens>
                      <apply>
                        <minus />
                        <apply>
                          <mult />
                          <apply>
                            <pow />
                            <id labels="VARIABLE" xml:space="preserve">τ</id>
                            <real>2</real>
                          </apply>
                          <id labels="*" xml:space="preserve">n</id>
                        </apply>
                        <real>1</real>
                      </apply>
                    </parens>
                    <apply>
                      <nthRoot />
                      <placeholder />
                      <apply>
                        <plus />
                        <apply>
                          <neg />
                          <parens>
                            <apply>
                              <mult />
                              <apply>
                                <pow />
                                <id labels="VARIABLE" xml:space="preserve">τ</id>
                                <real>2</real>
                              </apply>
                              <id labels="*" xml:space="preserve">m</id>
                            </apply>
                          </parens>
                        </apply>
                        <real>1</real>
                      </apply>
                    </apply>
                  </apply>
                  <apply>
                    <nthRoot />
                    <placeholder />
                    <apply>
                      <plus />
                      <apply>
                        <neg />
                        <apply>
                          <pow />
                          <id labels="VARIABLE" xml:space="preserve">τ</id>
                          <real>2</real>
                        </apply>
                      </apply>
                      <real>1</real>
                    </apply>
                  </apply>
                </apply>
              </apply>
            </apply>
          </lambda>
          <lowerBound>
            <real>0</real>
          </lowerBound>
          <upperBound>
            <apply>
              <id labels="FUNCTION" xml:space="preserve">sin</id>
              <id labels="*" xml:space="preserve">x</id>
            </apply>
          </upperBound>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

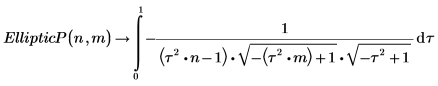
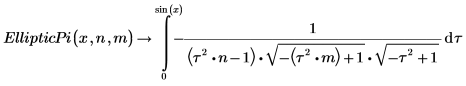
The two integrals are equal at x=π/2.