Example: Special Types of Matrices

Vectors, Matrices, and Tables > Working With Arrays > Example: Special Types of Matrices

This example illustrates a few special types of matrices.

Identity Matrices

An identity matrix is a square matrix where all elements along its diagonal are set to one and the remaining elements are set to zeros.

Use the identity function to generate a 3x3 identity matrix.

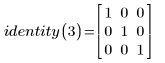
Diagonal Matrices

A diagonal matrix is a square matrix where all elements along its diagonal are set to any value and the remaining elements are set to zeros:

1. Define three input vectors:

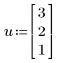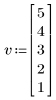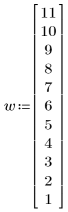2. Use the diag function to find the diagonal matrices formed from each vector:

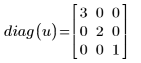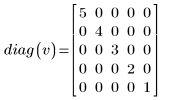The size of the generated square matrix is always nxn, where n is the length of the input vector.

3. Write a program for forming an upper triangular matrix:

<region id="ID0EJS2GB" top="912" left="48" width="347.389333318472" height="261.645333912969" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="Variable">upptriang</id>
        <boundVars>
          <id label="Variable">v</id>
        </boundVars>
      </function>
      <program>
        <localDefine>
          <id label="Variable">n</id>
          <apply>
            <id>ceil</id>
            <apply>
              <div />
              <apply>
                <plus />
                <real>-1</real>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <plus />
                    <real>1</real>
                    <apply>
                      <mult />
                      <real>8</real>
                      <apply>
                        <id>rows</id>
                        <id>v</id>
                      </apply>
                    </apply>
                  </apply>
                </apply>
              </apply>
              <real>2</real>
            </apply>
          </apply>
        </localDefine>
        <program>
          <localDefine>
            <apply>
              <indexer />
              <id label="Variable">M</id>
              <sequence>
                <apply>
                  <minus />
                  <id label="None">n</id>
                  <real>1</real>
                </apply>
                <apply>
                  <minus />
                  <id label="None">n</id>
                  <real>1</real>
                </apply>
              </sequence>
            </apply>
            <real>0</real>
          </localDefine>
          <localDefine>
            <id label="Variable">k</id>
            <real>0</real>
          </localDefine>
          <for>
            <id>i</id>
            <range>
              <sequence>
                <real>0</real>
                <real>1</real>
              </sequence>
              <apply>
                <minus />
                <id>n</id>
                <real>1</real>
              </apply>
            </range>
            <program>
              <for>
                <id>j</id>
                <range>
                  <sequence>
                    <id>i</id>
                    <apply>
                      <plus />
                      <id>i</id>
                      <real>1</real>
                    </apply>
                  </sequence>
                  <apply>
                    <minus />
                    <id>n</id>
                    <real>1</real>
                  </apply>
                </range>
                <program>
                  <if>
                    <test>
                      <apply>
                        <lessOrEqual />
                        <id>k</id>
                        <apply>
                          <minus />
                          <apply>
                            <id>rows</id>
                            <id>v</id>
                          </apply>
                          <real>1</real>
                        </apply>
                      </apply>
                    </test>
                    <then>
                      <program>
                        <localDefine>
                          <apply>
                            <indexer />
                            <id label="Variable">M</id>
                            <sequence>
                              <id label="None">i</id>
                              <id label="None">j</id>
                            </sequence>
                          </apply>
                          <apply>
                            <indexer />
                            <id>v</id>
                            <id>k</id>
                          </apply>
                        </localDefine>
                        <localDefine>
                          <id label="Variable">k</id>
                          <apply>
                            <plus />
                            <id>k</id>
                            <real>1</real>
                          </apply>
                        </localDefine>
                      </program>
                    </then>
                  </if>
                </program>
              </for>
            </program>
          </for>
        </program>
        <id>M</id>
      </program>
    </define>
  </math>
</region>

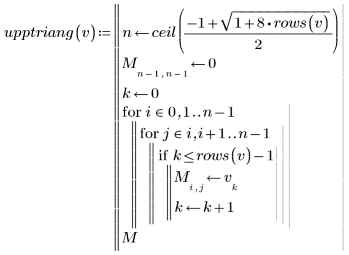
4. Use the program to generate the upper triangular matrix for each vector:

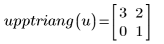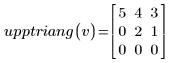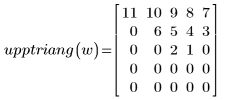The vector elements are placed in the output matrix starting from the diagonal element (0,0) and continuing to the right until row 0 is full, then from the diagonal element (1,1) until row 1 is full, and so on until the last element of the vector is placed. The size of the output square matrix is large enough to accommodate all elements of the vector.

5. Write a program for forming a lower triangular matrix:

<region id="ID0EMY2GB" top="1464" left="48" width="345.295999985139" height="261.645333912969" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math>
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id label="Variable">lowtriang</id>
        <boundVars>
          <id label="Variable">v</id>
        </boundVars>
      </function>
      <program>
        <localDefine>
          <id label="Variable">n</id>
          <apply>
            <id>ceil</id>
            <apply>
              <div />
              <apply>
                <plus />
                <real>-1</real>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <plus />
                    <real>1</real>
                    <apply>
                      <mult />
                      <real>8</real>
                      <apply>
                        <id>rows</id>
                        <id>v</id>
                      </apply>
                    </apply>
                  </apply>
                </apply>
              </apply>
              <real>2</real>
            </apply>
          </apply>
        </localDefine>
        <program>
          <localDefine>
            <apply>
              <indexer />
              <id label="Variable">M</id>
              <sequence>
                <apply>
                  <minus />
                  <id label="None">n</id>
                  <real>1</real>
                </apply>
                <apply>
                  <minus />
                  <id label="None">n</id>
                  <real>1</real>
                </apply>
              </sequence>
            </apply>
            <real>0</real>
          </localDefine>
          <localDefine>
            <id label="Variable">k</id>
            <real>0</real>
          </localDefine>
          <for>
            <id>i</id>
            <range>
              <sequence>
                <real>0</real>
                <real>1</real>
              </sequence>
              <apply>
                <minus />
                <id>n</id>
                <real>1</real>
              </apply>
            </range>
            <program>
              <for>
                <id>j</id>
                <range>
                  <sequence>
                    <real>0</real>
                    <real>1</real>
                  </sequence>
                  <id>i</id>
                </range>
                <program>
                  <if>
                    <test>
                      <apply>
                        <lessOrEqual />
                        <id>k</id>
                        <apply>
                          <minus />
                          <apply>
                            <id>rows</id>
                            <id>v</id>
                          </apply>
                          <real>1</real>
                        </apply>
                      </apply>
                    </test>
                    <then>
                      <program>
                        <localDefine>
                          <apply>
                            <indexer />
                            <id label="Variable">M</id>
                            <sequence>
                              <id label="None">i</id>
                              <id label="None">j</id>
                            </sequence>
                          </apply>
                          <apply>
                            <indexer />
                            <id>v</id>
                            <id>k</id>
                          </apply>
                        </localDefine>
                        <localDefine>
                          <id label="Variable">k</id>
                          <apply>
                            <plus />
                            <id>k</id>
                            <real>1</real>
                          </apply>
                        </localDefine>
                      </program>
                    </then>
                  </if>
                </program>
              </for>
            </program>
          </for>
        </program>
        <id>M</id>
      </program>
    </define>
  </math>
</region>

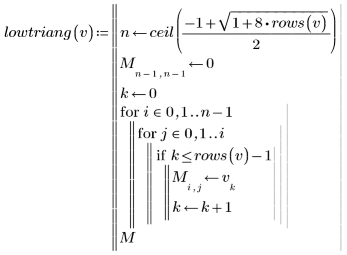
6. Use the program to generate lower triangular matrix for each vector:

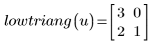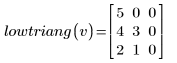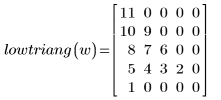The vector elements are placed in the output matrix starting from the diagonal element (0,0), then continuing down starting from element (1,0) until row 1 up to and including diagonal element (1,1) is full, then from element (2,0) until row 2 up to and including diagonal element (2,2) is full, and so on until the last element of the vector is placed. The size of the output square matrix is large enough to accommodate all elements of the vector.