Example: Factoring and Expanding Expressions
Use the keyword factor to find the factors of an integer, a radical expression, or an algebraic expression.
Use the keyword expand to expand expressions.
Factoring Integers
1. Define an integer.
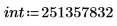
2. Insert the symbolic evaluation operator.
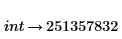
3. Type the keyword factor in the placeholder above the symbolic evaluation operator and press Enter.
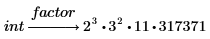
Factoring Radical Expressions
1. Define a radical expression.
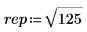
2. Insert the symbolic evaluation operator.
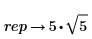
3. Type the keyword factor in the placeholder above the symbolic evaluation operator and press Enter.
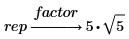
Factoring Polynomials
1. Define a polynomial in x.
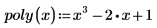
2. Insert the symbolic evaluation operator.
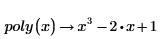
3. Type the keyword factor in the placeholder above the symbolic evaluation operator and press Enter.
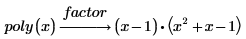
This keyword factors the polynomial over the rational numbers. In other words, the coefficients of the two factors are rational numbers (integers or ordinary fractions). You cannot factor the second term any further over the rational numbers, because its roots involve the square root of 5, which is irrational.
4. Find the roots using the keyword solve, which returns the roots in a vector.
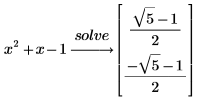
5. To factor the original polynomial completely over the real numbers, add the radical expression square root of 5 as an argument by typing a comma after factor and then typing square root of 5 in the placeholder that appears after the comma.
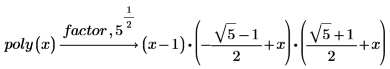
In general, using the keyword factor with no additional arguments factors a polynomial over the field of numbers generated by its coefficients. That is, if the coefficients of polynomial are all rational numbers, the coefficients of the factors must all be rational. However, if the coefficients of the polynomial include a radical expression, the coefficients of the factors can also contain the same radical expression. |
Expanding Expressions
1. Use the expand keyword to expand the following expression:
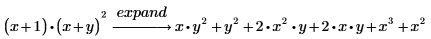
2. Type a comma after expand, then type a subexpression of the main expression.
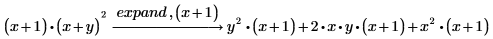
PTC Mathcad expands all terms except for the subexpression.
3. Type a subexpression that is not in the original expression.
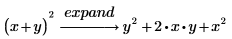
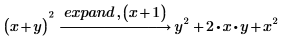
The result is the same as if you had not included the modifier.
Factoring Polynomials Completely over the Real Numbers
1. Use the keyword solve to find the real coefficients of this polynomial over the real numbers.
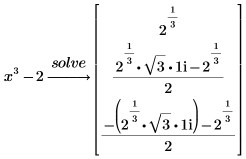
2. Replace the keyword solve with factor and type a comma-separated list of all the radicals appearing in the roots of the polynomial.
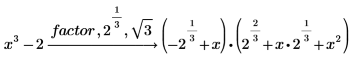
Factoring the Polynomial Completely over the Complex Numbers
1. To factor any polynomial completely over the complex numbers, add the complex number 1i to the list of radicals.
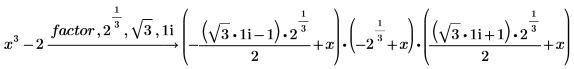
2. Alternatively, define a vector by the symbolic roots and then insert entries of the vector after factor.
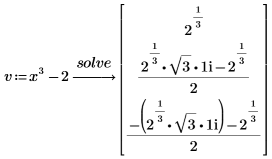
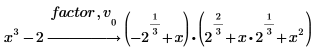
Since v0 contains both radicals appearing in the roots, as well as i, you only need to enter one of the roots.
3. Factor a polynomial over the real or complex numbers into terms with floating-point coefficients, rather than symbolic ones, using the modifiers real or complex.
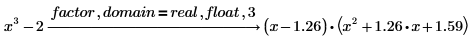
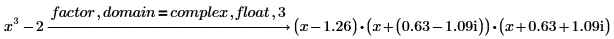
The keyword float is used to reduce the number of decimal places displayed in the coefficients.