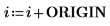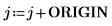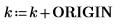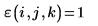Vectors, Matrices, and Tables > Working With Arrays > Example: Effect of ORIGIN on non-Lookup Functions
Example: Effect of ORIGIN on non-Lookup Functions
The system variable ORIGIN affects the result of three functions that operate on arrays: submatrix, csort and rsort.
It also affects one function that does not operate on arrays: e (the antisymmetric tensor function).
1. Define an input matrix.
Click to copy this expression
2. Evaluate ORIGIN to ensure that it is set to 0.
Click to copy this expression
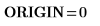
ORIGIN=0: submatrix, csort and rsort
1. Define the row and column arguments.
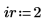
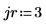
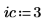
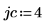
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
2. Use the submatrix function to extract a submatrix from matrix M.
Click to copy this expression
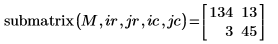
The result is the submatrix found between rows 2 and 3 and columns 3 and 4.
3. Define the column argument and evaluate the column sort function csort.
Click to copy this expression
Click to copy this expression
The returned matrix is the result of rearranging the rows of M until column 3 is in ascending order.
4. Define the row argument and evaluate the row sort function rsort.
Click to copy this expression
Click to copy this expression
The returned matrix is the result of rearranging the columns of M until row 4 is in ascending order.
ORIGIN=1: submatrix, csort and rsort
1. Set ORIGIN to 1.
Click to copy this expression
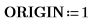
2. Reevaluate the submatrix function.
Click to copy this expression
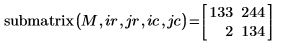
The returned matrix now comes from rows 1 and 2 and columns 2 and 3.
3. Show that in order to get the same results when ORIGIN is set to 0, you must add the new value of ORIGIN to the row and column indices of the submatrix function.
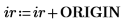
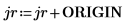
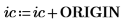
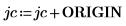
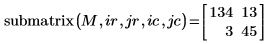
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
4. Reevaluate the csort function.
Click to copy this expression
The returned matrix now shows that column 2, and not 3, is in ascending order.
5. Show that in order to get the same results when ORIGIN is set to 0, you must add the new value of ORIGIN to the c argument.
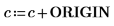
Click to copy this expression
Click to copy this expression
6. Reevaluate the rsort function.
Click to copy this expression
The returned matrix shows that row 3, and not 4, is in ascending order.
7. Show that in order to get the same results when ORIGIN is set to 0, you must add the new value of ORIGIN to the r argument.
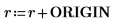
Click to copy this expression
Click to copy this expression
ORIGIN=0: e
1. Set ORIGIN to 0.
Click to copy this expression
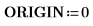
2. Define the three arguments of the antisymmetric tensor function, i, j and k.
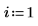
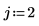
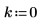
Click to copy this expression
Click to copy this expression
Click to copy this expression
3. Evaluate the antisymmetric tensor function ε.
Click to copy this expression
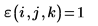
ORIGIN=1: e
1. Set ORIGIN to 1.
Click to copy this expression
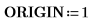
2. Reevaluate the antisymmetric tensor function.
Click to copy this expression
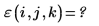
The error occurs because the value of each argument must be between ORIGIN and ORIGIN+2.
3. Show that in order to get the same results when ORIGIN is set to 0, you must add the new value of ORIGIN to each of the three arguments.
Click to copy this expression
Click to copy this expression
Click to copy this expression
Click to copy this expression
To Set the Array ORIGIN
About Functions for Creating and Subdividing Arrays
Antisymmetric Tensor Function
Sorting Arrays
Was this helpful?