Example: Adding Units to Solve Blocks

Solve Blocks > Example: Adding Units to Solve Blocks

You can add units to solve blocks. You must ensure that the units are compatible with one another throughout your calculations.

1. Define the length of a pendulum.

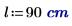
2. Insert a solve block, define a differential equation for the problem, and use the odesolve function to solve the equation. Angle Ɵ is the angle between the vertical and the pendulum.

<region id="ID0EKI4JB" actualWidth="233" actualHeight="221.39999999999998" top="230.40000000000003" left="38.400000000000006" height="221.39999999999998" width="233" xmlns="http://schemas.mathsoft.com/worksheet50">
 <solveblock>
 <regions>
 <region id="" actualWidth="174.87333333333333" actualHeight="56.369333557128911" top="43.2" left="24" solve-block-category="constraint">
 <math resultRef="92">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <equal />
 <apply>
 <derivative />
 <lambda>
 <boundVars>
 <id xml:space="preserve">t</id>
 </boundVars>
 <apply>
 <id xml:space="preserve">θ</id>
 <id xml:space="preserve">t</id>
 </apply>
 </lambda>
 <degree>
 <real>2</real>
 </degree>
 </apply>
 <apply>
 <mult />
 <apply>
 <neg />
 <apply>
 <div />
 <id labels="UNIT" xml:space="preserve">g</id>
 <id xml:space="preserve">l</id>
 </apply>
 </apply>
 <apply>
 <id xml:space="preserve">sin</id>
 <apply>
 <id xml:space="preserve">θ</id>
 <id xml:space="preserve">t</id>
 </apply>
 </apply>
 </apply>
 </apply>
 </math>
 </region>
 <region id="" actualWidth="61.693333333333342" actualHeight="25.6" top="96" left="24" solve-block-category="constraint">
 <math resultRef="94">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <equal />
 <apply>
 <id xml:space="preserve">θ</id>
 <real>0</real>
 </apply>
 <real>0</real>
 </apply>
 </math>
 </region>
 <region id="" actualWidth="64.786666666666676" actualHeight="25.6" top="144" left="24" solve-block-category="constraint">
 <math resultRef="96">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <equal />
 <apply>
 <apply>
 <functionDerivative />
 <id xml:space="preserve">θ</id>
 </apply>
 <real>0</real>
 </apply>
 <real>2</real>
 </apply>
 </math>
 </region>
 <region id="" actualWidth="164.43666666666667" actualHeight="25.6" top="196.8" left="24" solve-block-category="solver">
 <math resultRef="98">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">Θ</id>
 <apply>
 <id labels="KEYWORD" xml:space="preserve">odesolve</id>
 <sequence>
 <apply>
 <id xml:space="preserve">θ</id>
 <id xml:space="preserve">t</id>
 </apply>
 <real>10</real>
 </sequence>
 </apply>
 </define>
 </math>
 </region>
 </regions>
 </solveblock>
</region>

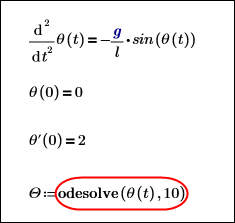
Both the length l and the gravitational constant g have units:

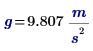
However, the initial conditions and the terminal point do not have units. As a result, the error about unit compatibility appears.

3. Add compatible units to all solve block components.

<region id="ID0EZK4JB" actualWidth="233" actualHeight="223" top="614.40000000000009" left="38.400000000000006" height="223" width="233" xmlns="http://schemas.mathsoft.com/worksheet50">
 <solveblock>
 <regions>
 <region id="" actualWidth="174.87333333333333" actualHeight="56.369333557128911" top="43.2" left="24" solve-block-category="constraint">
 <math resultRef="102">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <equal />
 <apply>
 <derivative />
 <lambda>
 <boundVars>
 <id xml:space="preserve">t</id>
 </boundVars>
 <apply>
 <id xml:space="preserve">θ</id>
 <id xml:space="preserve">t</id>
 </apply>
 </lambda>
 <degree>
 <real>2</real>
 </degree>
 </apply>
 <apply>
 <mult />
 <apply>
 <neg />
 <apply>
 <div />
 <id labels="UNIT" xml:space="preserve">g</id>
 <id xml:space="preserve">l</id>
 </apply>
 </apply>
 <apply>
 <id xml:space="preserve">sin</id>
 <apply>
 <id xml:space="preserve">θ</id>
 <id xml:space="preserve">t</id>
 </apply>
 </apply>
 </apply>
 </apply>
 </math>
 </region>
 <region id="" actualWidth="73.346666666666678" actualHeight="25.6" top="96" left="24" solve-block-category="constraint">
 <math resultRef="104">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <equal />
 <apply>
 <id xml:space="preserve">θ</id>
 <apply>
 <scale />
 <real>0</real>
 <id xml:space="preserve">s</id>
 </apply>
 </apply>
 <real>0</real>
 </apply>
 </math>
 </region>
 <region id="" actualWidth="104.56" actualHeight="29.752000000000002" top="144" left="24" solve-block-category="constraint">
 <math resultRef="106">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <equal />
 <apply>
 <apply>
 <functionDerivative />
 <id xml:space="preserve">θ</id>
 </apply>
 <apply>
 <scale />
 <real>0</real>
 <id xml:space="preserve">s</id>
 </apply>
 </apply>
 <apply>
 <mult />
 <real>2</real>
 <apply>
 <pow />
 <id xml:space="preserve">s</id>
 <real>-1</real>
 </apply>
 </apply>
 </apply>
 </math>
 </region>
 <region id="" actualWidth="176.67666666666668" actualHeight="25.6" top="196.8" left="24" solve-block-category="solver">
 <math resultRef="108">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">Θ</id>
 <apply>
 <id labels="KEYWORD" xml:space="preserve">odesolve</id>
 <sequence>
 <apply>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">θ</id>
 <id xml:space="preserve">t</id>
 </apply>
 <apply>
 <scale />
 <real>10</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </sequence>
 </apply>
 </define>
 </math>
 </region>
 </regions>
 </solveblock>
</region>

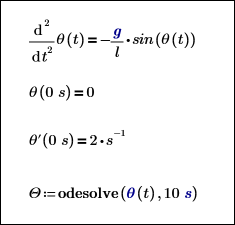
4. Define a range of values over which to plot the solve block solution. You must use the step range operator when you define ranges with units.

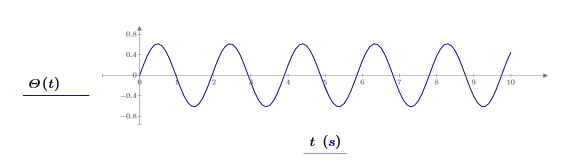
5. Plot the solve block solution.

<region id="ID0EZN4JB" actualWidth="576" actualHeight="168.00000000000003" top="998.40000000000009" left="38.400000000000006" height="168.00000000000003" width="576" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="112">
 <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="460.8" height="110.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="10">
 <axisLine position="origin" positionticmark="2" legendWidth="60.71" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="113">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">t</id>
 </math>
 <math resultRef="114">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.8" end="0.8">
 <axisLine position="origin" positionticmark="0" legendWidth="84.5333333333333" />
 <axisGrid>
 <gridFrequency>5</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="119">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Θ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
 </apply>
 </math>
 <math resultRef="120">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="116">
 <real xmlns="http://schemas.mathsoft.com/math50">-0.8</real>
 </startValue>
 <secondTickValue resultRef="118">
 <real xmlns="http://schemas.mathsoft.com/math50">-0.4</real>
 </secondTickValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>

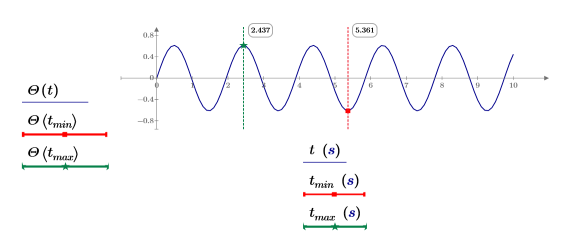
6. Construct a solve block, and then use the minimize function to find when Ɵ is at its minimum given a guess value of t=5 s.

<region id="ID0E3P4JB" actualWidth="300" actualHeight="100" top="1209.6000000000001" left="38.400000000000006" height="100" width="300" xmlns="http://schemas.mathsoft.com/worksheet50">
 <solveblock>
 <regions>
 <region id="" actualWidth="50.683333333333337" actualHeight="25.6" top="38.400000000000006" left="19.200000000000003" solve-block-category="guess-value">
 <math resultRef="127">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">t</id>
 <apply>
 <scale />
 <real>5</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </define>
 </math>
 </region>
 <region id="" actualWidth="218.85999999999999" actualHeight="27.791200000000003" top="76.800000000000082" left="19.200000000000003" solve-block-category="solver">
 <math resultRef="129">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="*" xml:space="preserve">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">min</Subscript>
 </id>
 <eval>
 <apply>
 <id labels="KEYWORD" xml:space="preserve">minimize</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Θ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 </math>
 </region>
 </regions>
 </solveblock>
</region>

The units of the guess value must be compatible with the definition of the function to minimize.

7. Construct a solve block, and then use the maximize function to find when Ɵ is at its maximum given a guess value of t=2 s and a constraint of t<4 s.

<region id="ID0EIS4JB" actualWidth="311.96333333333337" actualHeight="135" top="1440.0000000000002" left="38.400000000000006" height="135" width="311.96333333333337" xmlns="http://schemas.mathsoft.com/worksheet50">
 <solveblock>
 <regions>
 <region id="" actualWidth="50.683333333333337" actualHeight="25.6" top="38.400000000000006" left="19.200000000000003" solve-block-category="guess-value">
 <math resultRef="131">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">t</id>
 <apply>
 <scale />
 <real>2</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
 </region>
 <region id="" actualWidth="48.513333333333335" actualHeight="25.6" top="76.800000000000011" left="19.200000000000003" solve-block-category="constraint">
 <math resultRef="133">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <lessThan />
 <id labels="VARIABLE" xml:space="preserve">t</id>
 <apply>
 <scale />
 <real>4</real>
 <id labels="UNIT" xml:space="preserve" label-is-contextual="true">s</id>
 </apply>
 </apply>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
 </region>
 <region id="" actualWidth="223.94666666666669" actualHeight="27.791200000000003" top="115.20000000000002" left="19.200000000000003" solve-block-category="solver">
 <math resultRef="135">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="*" xml:space="preserve">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">max</Subscript>
 </id>
 <eval>
 <apply>
 <id labels="KEYWORD" xml:space="preserve">maximize</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Θ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
 </region>
 </regions>
 </solveblock>
</region>

8. Use the SIUnitsOf function to strip the unit from the maxima and minima points. This is required in order to use the unitless vertical markers.

<region id="ID0EHU4JB" actualWidth="230.05666666666667" actualHeight="51.582400000000007" top="1689.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="137">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">max</id>
 <eval>
 <apply>
 <div />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">max</Subscript>
 </id>
 <apply>
 <id labels="FUNCTION" xml:space="preserve">SIUnitsOf</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">max</Subscript>
 </id>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 </math>
</region>

<region id="ID0EVU4JB" actualWidth="226.24666666666664" actualHeight="51.582400000000007" top="1766.4000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="139">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">min</id>
 <eval>
 <apply>
 <div />
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">min</Subscript>
 </id>
 <apply>
 <id labels="FUNCTION" xml:space="preserve">SIUnitsOf</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">min</Subscript>
 </id>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 </math>
</region>

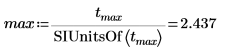
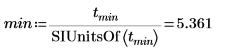
9. Show the maxima and minima points on the original plot. Use vertical markers to show where these two points intersect the time axis.

<region id="ID0EFW4JB" actualWidth="577.2" actualHeight="244.80000000000004" top="1881.6000000000004" left="38.400000000000006" height="244.80000000000004" width="577.2" xmlns="http://schemas.mathsoft.com/worksheet50">
 <plot background-type="white" origin-positioning="true">
 <xyPlot>
 <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
 <legend />
 <traces>
 <trace resultRef="141">
 <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="142">
 <traceStyle color="#FFFF0000" symbol="filledRectangle" line-weight="2" line-style="Solid">lines</traceStyle>
 </trace>
 <trace resultRef="143">
 <traceStyle color="#FF068149" symbol="filledStar" line-weight="2" line-style="Solid">lines</traceStyle>
 </trace>
 </traces>
 <graph-size width="442.8" height="110.4" />
 <axes>
 <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="10">
 <axisLine position="origin" positionticmark="2" legendWidth="81.8666666666667" />
 <axisGrid>
 <gridFrequency>11</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers>
 <marker resultRef="144" display="true" color="#FF068149" line-style="Dash" value="2.4368823377188966">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">max</id>
 </marker>
 <marker resultRef="146" display="true" color="#FFED1D2F" line-style="Dash" value="5.3611508941582011">
 <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">min</id>
 </marker>
 </markers>
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="148">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">t</id>
 </math>
 <math resultRef="149">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="150">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">min</Subscript>
 </id>
 </math>
 <math resultRef="151">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="152">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">max</Subscript>
 </id>
 </math>
 <math resultRef="153">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </startValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </xAxis>
 <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.8" end="0.8">
 <axisLine position="origin" positionticmark="0" legendWidth="105.763333333333" />
 <axisGrid>
 <gridFrequency>5</gridFrequency>
 <gridLabels display="true" />
 <gridLines />
 <tickMarks display="true" />
 </axisGrid>
 <axisLabel />
 <markers />
 <numberFormat>
 <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
 </numberFormat>
 <plotEquations>
 <plotEquation>
 <math resultRef="158">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Θ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
 </apply>
 </math>
 <math resultRef="159">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="160">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Θ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">min</Subscript>
 </id>
 </apply>
 </math>
 <math resultRef="161">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 <plotEquation>
 <math resultRef="162">
 <apply xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Θ</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 t<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">max</Subscript>
 </id>
 </apply>
 </math>
 <math resultRef="163">
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </math>
 </plotEquation>
 </plotEquations>
 <xyDomain scale-type="linear" auto-scale="true">
 <startValue resultRef="155">
 <real xmlns="http://schemas.mathsoft.com/math50">-0.8</real>
 </startValue>
 <secondTickValue resultRef="157">
 <real xmlns="http://schemas.mathsoft.com/math50">-0.4</real>
 </secondTickValue>
 <endValue>
 <placeholder xmlns="http://schemas.mathsoft.com/math50" />
 </endValue>
 </xyDomain>
 </yAxis>
 </axes>
 </xyPlot>
 </plot>
</region>