Beispiel: Symbolische elliptische Integralfunktionen
Die folgenden elliptischen Integralfunktionen sind in vielen symbolischen Berechnungen enthalten.
|
|
Die elliptischen Integralfunktionen sind nicht Teil des PTC Mathcad Prime Satzes vordefinierter Funktionen.
|
EllipticK: vollständiges elliptisches Integral erster Art
1. Zeigen Sie die Definition des vollständigen elliptischen Integrals erster Art EllipticK(m) an.
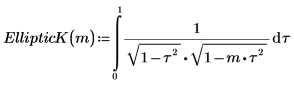
2. Werten Sie EllipticK numerisch aus.
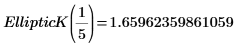
3. Plotten Sie die numerischen Werte von EllipticK im Bereich von 0<m<1.
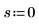 | 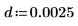 | 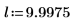 |
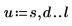 | ||
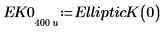 | 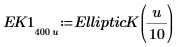 | |
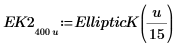 | 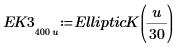 |
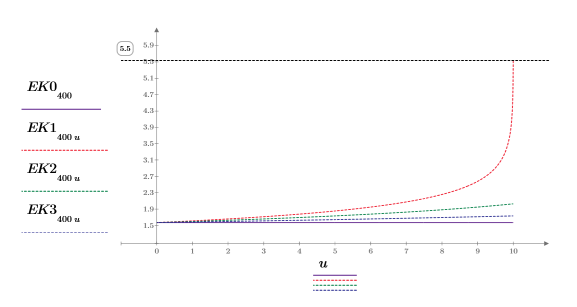
Das Integral ist gleich π/2, wenn m=0, und nähert sich 12 an, wenn m sich 1 annähert. Die horizontale Markierung zeigt den Wert von Elliptick(l/10) an, oder:
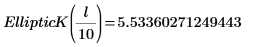
EllipticF: unvollständiges elliptisches Integral erster Art
1. Zeigen Sie die Definition des unvollständigen elliptischen Integrals erster Art EllipticF(x, m) an.
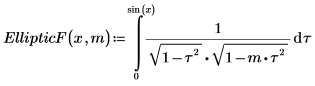
2. Werten Sie EllipticF numerisch aus.
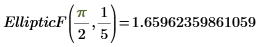
3. Zeigen Sie die Beziehung zwischen EllipticF und EllipticK an.
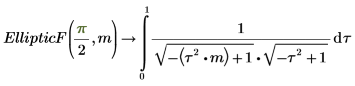
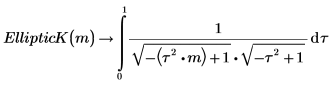
Die beiden Integrale sind gleich.
EllipticE: elliptisches Integral zweiter Art
1. Zeigen Sie die Definition des vollständigen elliptischen Integrals zweiter Art EllipticE(m) an:
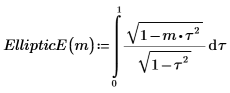
Alternativ wird die Funktion angegeben durch:
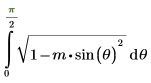
2. Werten Sie EllipticE numerisch aus.
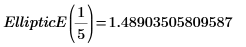
3. Zeigen Sie die Definition des unvollständigen elliptischen Integrals zweiter Art EllipticE(x, m) an:
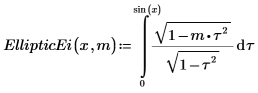
4. Werten Sie EllipticEi numerisch aus.
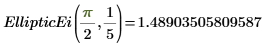
5. Zeigen Sie die Beziehung zwischen EllipticE und EllipticEi an.
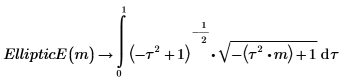
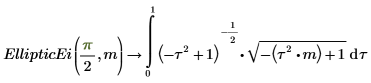
Die beiden Integrale sind gleich.
EllipticP: elliptisches Integral dritter Art
1. Zeigen Sie die Definition des vollständigen elliptischen Integrals dritter Art EllipticPi(n, m) an:
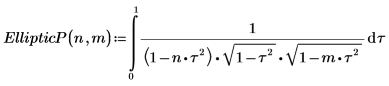
2. Werten Sie EllipticP(n, m) numerisch aus.
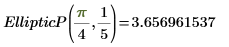
3. Zeigen Sie die Definition des unvollständigen elliptischen Integrals dritter Art EllipticPi(x, n, m) an:
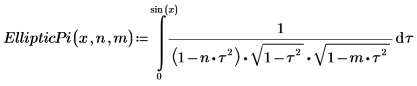
4. Werten Sie EllipticPi numerisch aus.
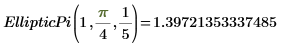
5. Zeigen Sie die Beziehung zwischen EllipticP und EllipticPi an.
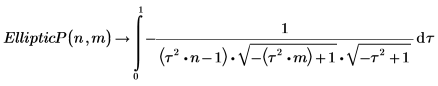
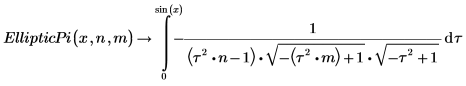
Die beiden Integrale sind gleich bei x=π/2.