Beispiel: Symbolische Analysis II
Lösen Sie symbolische Probleme in der Analysis, indem Sie den Ausdruck für das Problem mit dem symbolischen Auswertungsoperator auswerten und Schlüsselwörter hinzufügen, um das Problem ggf. zu ändern.
Taylor- und Maclaurin-Reihe
1. Verwenden Sie das Schlüsselwort series, um die Funktion sin in einer Maclaurin-Reihe zu erweitern.
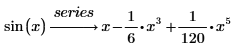
Standardmäßig gibt PTC Mathcad die Ausdrücke bis zur Ordnung 6 zurück, sodass die höchste Potenz der Antwort 5 ist. |
2. Geben Sie nach series ein Komma und anschließend x, 10 in den Platzhalter ein, um die Ordnung der Ausdrücke auf 10 zu erhöhen.
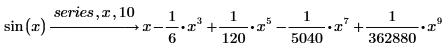
3. Erweitern Sie die Funktion sin zur einer Taylor-Reihe um 1.
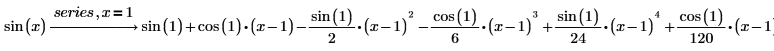
4. Erweitern Sie eine Funktion in mehr als einer Variablen um den Punkt (x, y)=(0, 1).
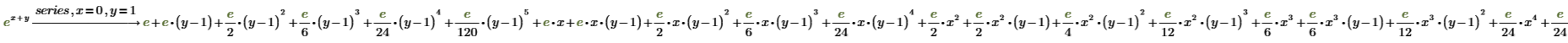
5. Zeigen Sie die Koeffizienten als vierstellige Zahlen statt bezogen auf e an.
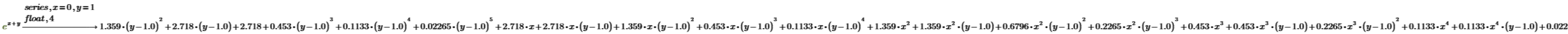
Partialbrüche
1. Führen Sie mit dem Schlüsselwort parfrac eine Partialbruchzerlegung einer rationalen Funktion (Quotient von Polynomen) durch.
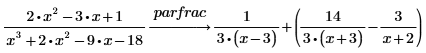
2. Führen Sie eine Partialbruchzerlegung einer Funktion durch, die über den Bereichsproduktoperator definiert ist.
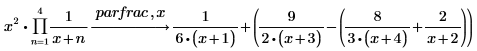
Zerlegung über die reellen oder komplexen Zahlen
Standardmäßig führt PTC Mathcad die Partialbruchzerlegung über den Bereich rationaler Zahlen durch. Das bedeutet Folgendes: Wenn der anfängliche Ausdruck ein Quotient von Polynomen mit rationalen Koeffizienten ist, haben die Polynome im Ergebnis ebenfalls rationale Koeffizienten.
1. Verwenden Sie das Schlüsselwort parfrac, um Brüche der folgenden Funktion zu ermitteln.
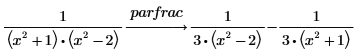
2. Führen Sie eine weitere Zerlegung eines der Ausdrücke in folgenden Ausdrücken durch:
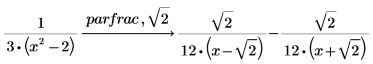
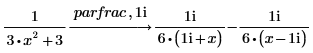
3. Führen Sie eine vollständige Partialbruchzerlegung einer rationalen Funktion über die komplexen Zahlen durch, indem Sie domain = complex nach parfrac eingeben.
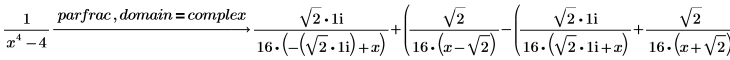
Führen Sie die folgenden Schritte aus, um eine Zerlegung über die reellen Zahlen zu erhalten: a. Kombinieren Sie die beiden letzten Ausdruck zu einem einzigen Ausdruck mit reellen Koeffizienten, indem Sie das Schlüsselwort simplify wie folgt verwenden: 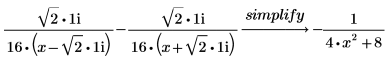 b. Ersetzen Sie die vereinfachten Ergebnisse in den ursprünglichen Ergebnissen, um folgendes Ergebnis zu erhalten: 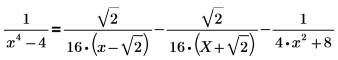 |
Kettenbrüche
1. Verwenden Sie das Schlüsselwort confrac, um die Kettenbruchentwicklung einer Zahl zu ermitteln.
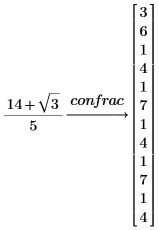
2. Mit dem Modifizierer fraction sehen Sie den eigentlichen Kettenbruch statt des Vektors.
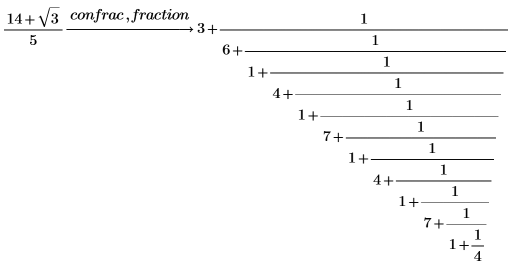
Standardmäßig gibt PTC Mathcad genügend Ausdrücke des Kettenbruchs zurück, sodass die Antwort auf 10 signifikante Stellen genau ausfällt. |
3. Fügen Sie eine positive Ganzzahl hinzu, die die Zahl der signifikanten Stellen angibt, um Ergebnisse mit einem unterschiedlichen Genauigkeitsgrad zurückzugeben.
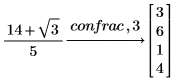

4. Erweitern Sie die Funktion sin als Kettenbruch.
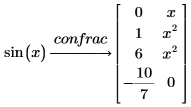
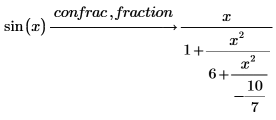
PTC Mathcad gibt eine zweite Spalte mit den Potenzen von x zurück, die den Ausdrücken entsprechen. |