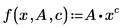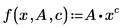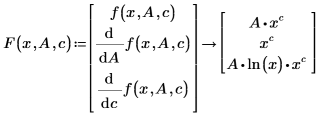非線性遞歸
• genfit(vx, vy, vg, F) - 傳回向量,其內含 的參數,可產生x的 F函數及n參數 u1... un ,最近似於 vx 及 vy.中的數據。
genfit 函數會利用最佳化版本的雷文柏格-馬括特方法,進行最小化處理。雖然速度較快而且較不受較差估值的影響,但是此實行可能會無法適當地收斂許多局部最小值問題 (如有理函數),此實行對不正確的導數向量很敏感。
引數
• vx, vy 是長度相同之實數數據值的向量,分別對應至數據集中的 x 與 y 值。數據點數至少必須與參數的數目相同。
• vg 是參數估值的 n 元素向量。若 n = 1,則 vg 為純量。
• F(x, u) 是擬合函數或函數向量,其中 x 是自變數,而 u 是參數向量或個別參數名稱。下列方程式是擬合函數的有效表示:
• n 是正整數。若是非向量化參數,則會有九個個別名稱的限制。
改進收斂度
若要改進收斂度,以及盡可能改進 genfit 的精確度,您可以函數的 n+1 向量來代表 F,其中第一個項目 F0 為擬合函數 f,而其餘項目 F1、F2、...、Fn 為相對於 n 參數之 f 的符號偏導數。
在上述代表擬合函數的兩種方式中,若以符號方式求解偏導數,則只能使用 f(x,A,c) 。因此,以函數向量代表 F 時,n 的限制為 9,因此 F 的最大長度為 10。您可以建構以適當的偏導數所組成的矩陣,然後以符號方式進行計算,藉此建立向量 F。
其他資訊
• 您僅可提供擬合函數或函數向量的名稱給 genfit,而不提供任何引數。
• 若使用擬合函數但不提供符號參數偏導數,則 genfit 會以數值方式計算參數偏導數。這比提供符號導數更不精確,但在某些情況下可能會很方便。
• 若 genfit 無法轉換,則您可以嘗試其他估值,或調整數據讓所有參數的量值順序類似。與所有數值解技巧相同,非線性問題非常容易受到估值的影響。
• 您可以使用估值繪製擬合函數,以協助您精簡估值,再使用 genfit。
• 最佳化的雷文柏格-馬括特方法比較容易受到所提供之代數導數中錯誤的影響。若 genfit 失敗,您應該檢查導數運算式。