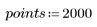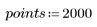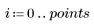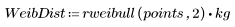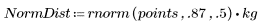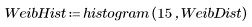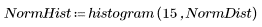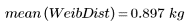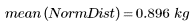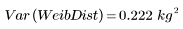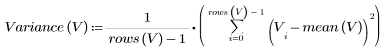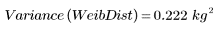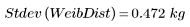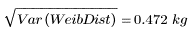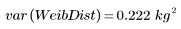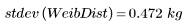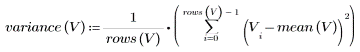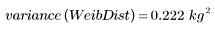範例:變異數與標準差
使用
Var 與
Stdev 函數比較韋伯分佈與常態分佈之分佈。
1. 定義根據韋伯分佈與常態分佈的數據集。
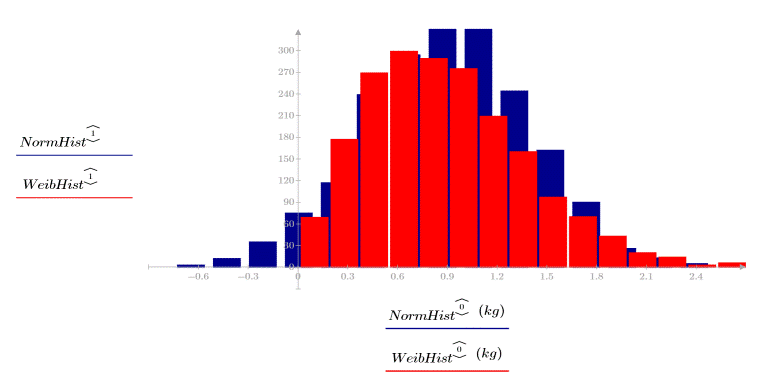
2. 繪製分佈。
兩個數據集的均數雖然類似,但分佈與形狀不同:
3. 計算分佈的取樣變異數。
韋伯分佈的變異數較小,表示常態分佈的分佈較低。
取樣變異數的計算如下:
4. 計算韋伯分佈的取樣標準差。
標準差的單位與原始數據的單位相同,使其成為比變異數更直覺式的散佈量測。可視為一連串實際上應完全相同的量測之誤差量測。
取樣標準差是取樣變異數的平方根。
5. 計算韋伯分佈的總體變異數與標準差:
總體變異數與標準差會除以樣本大小,而不是除以樣本大小減一:
| 取樣標準差 (或函數 Var) 是量化數據分析中比較常用的定義。 |