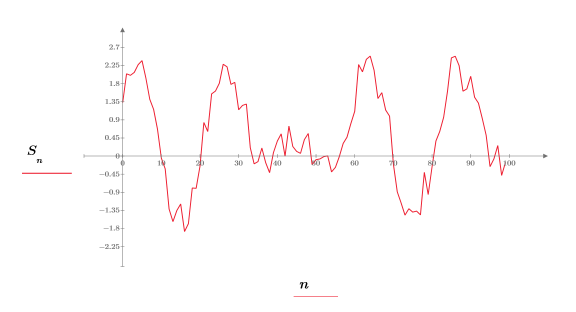
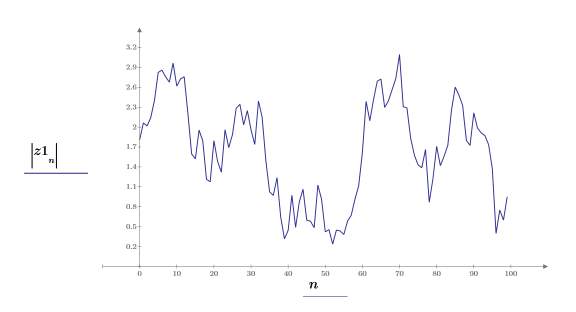
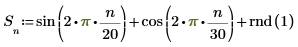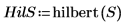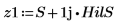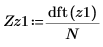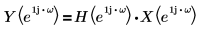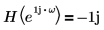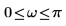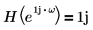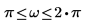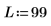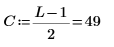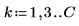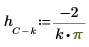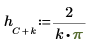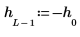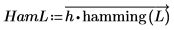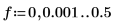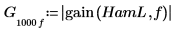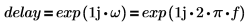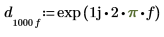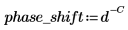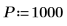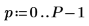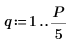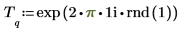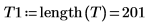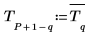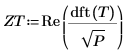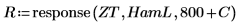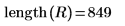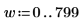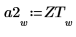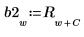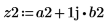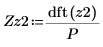範例:希爾伯特轉換
使用
hilbert 函數建立實數信號的希爾伯特轉換,使分析信號的離散傅立葉轉換在負數頻率上的量值為零。
2.
3. hilbert 函數計算輸入信號的希爾伯特轉換。
4.
5.
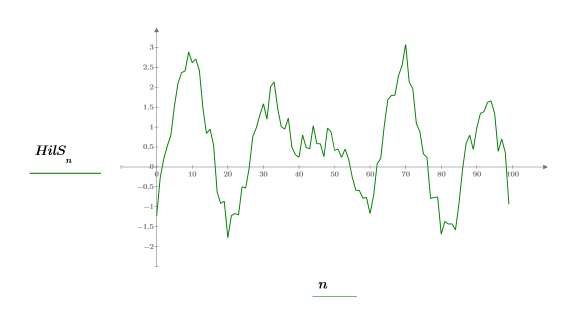
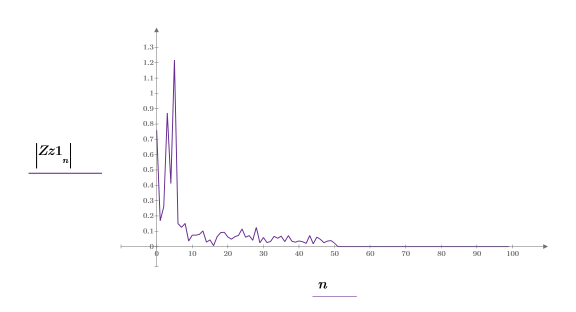
後續步驟顯示分析信號的量值為原始信號的複數包絡。
7.
對於向量而言,介於 dft 函數與已取代的 CFFT 函數之間的縮放係數為 1/N 。
8.
希爾伯特建立的新信號與輸入信號在轉換區域中以下列方式相互關聯:
其中 H 又稱為希爾伯特轉換器,是使用頻率回應的濾波器:
您可以透過濾波器設計程序與函數建構 H 。
典型的希爾伯特轉換器
Rabiner 與 Gold 合著的 Theory and Application of Digital Signal Processing (數位信號處理的理論與應用) (Prentice-Hall, Inc.) 中提供典型希爾伯特轉換器的係數。下列範例以 Stearns 與 David 合著的 Signal Processing Algorithms (信號處理演算法) (Prentice-Hall) 第 14.4 節的使用方式為基礎。典型濾波器的係數會加窗並會位移,以取得奇數長度 L 的不正式濾波。
1.
2. h 。
3. 使用
hamming 函數以漢明窗為係數加窗,並使用
vectorize 運算子逐元素乘以
h 與視窗。
4. 使用
gain 函數透過係數
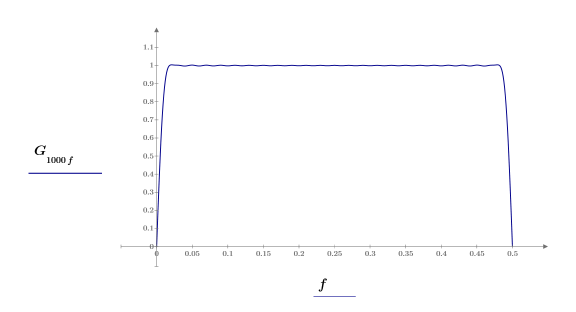
h 計算濾波器在頻率
f 時的增量。
5.
頻率會常態化為取樣頻率 1。
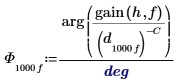
濾波器具有 C 的延遲,因此我們會計算延遲信號的相對濾波器之相角位移。延遲具有該轉移函數:
7.
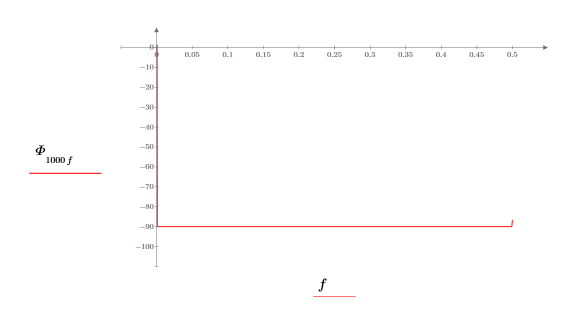
幾乎整個頻率範圍的位移皆為 -90 度以上。
檢驗濾波器
1.
2. exp 函數建立新信號。使用 rnd 函數加入低頻雜訊。
您可以將游標置於 rnd 上並按 F5 鍵,重新計算並獲得不同的隨機信號 T 。
3.
新的向量具有 1001 個元素,其中 1-200 個元素包含原始向量 T ,而 801-1000 個元素包含 T 的共軛。中間元素設置為 0。
4. T 信號的傅立葉轉換。
使用
Re 函數移除小的虛數捨入誤差。雜訊會透過建構其轉換 T 所產生,並使用第一個元素之後的前 200 個元素的隨機相角與單位量值。
5.
7. ZT 的前 800 個元素與 R 的後 800 個元素建立複數信號 z2 。
將傅立葉轉換向量 ZT 的前 800 個儲存為向量 a2 。
將回應向量 R 的後 800 個元素儲存為向量 b2 。
定義複數信號 z2 。
8. dft 函數計算信號 z2 的離散傅立葉轉換。
對於向量而言,介於 dft 函數與已取代的 CFFT 函數之間的縮放係數為 1/P 。
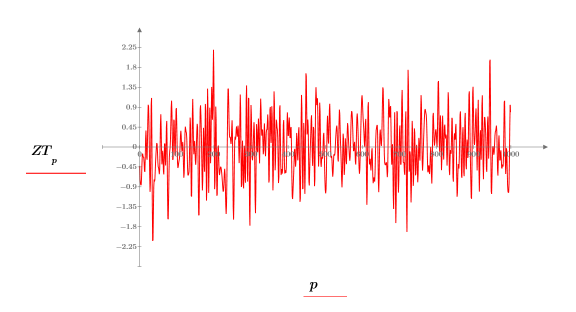
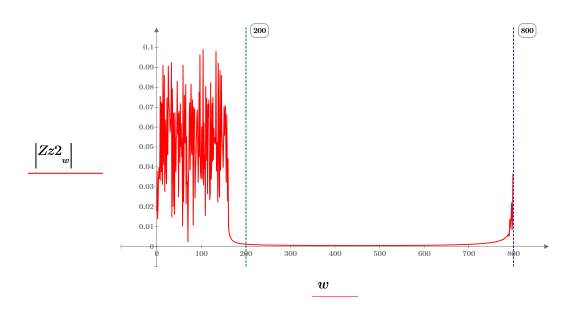
9. z2 的離散傅立葉轉換的絕對值。
上圖顯示用以在轉換區域中產生信號的原始 200 個點。頻譜的上半部份基本上為零,由此得知希爾伯特轉換器濾波已確實執行。
複製運算式