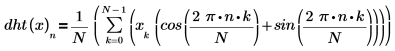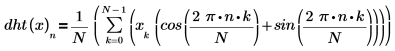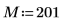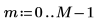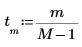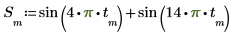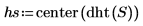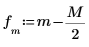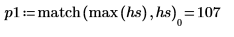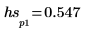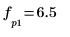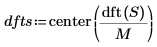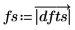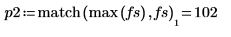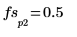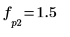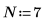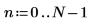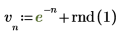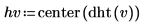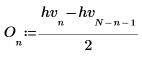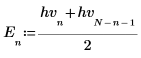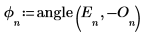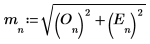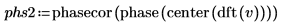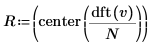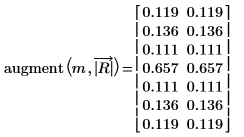範例:哈特利轉換
為哈特利轉換定義的總和類似離散傅立葉轉換總和。
其中 N 是實數數據陣列 x 的元素數。
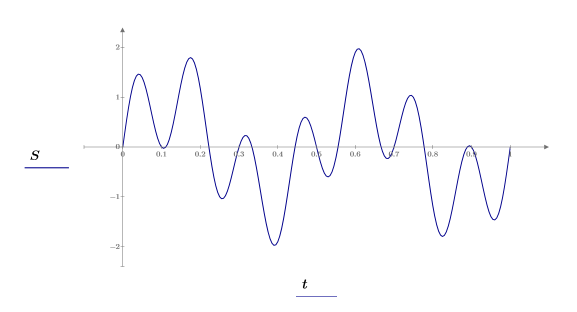
正弦波的總和
求解正弦波總和的哈特利轉換,並將其與複數傅利葉轉換的量值進行比較。
1. 定義元素數。
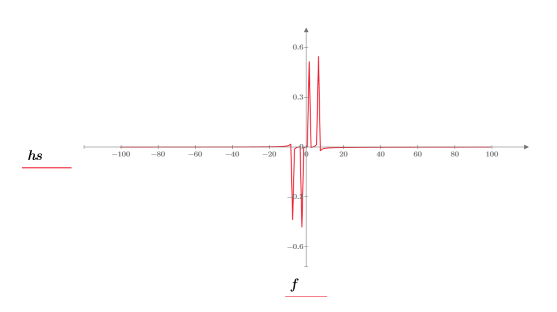
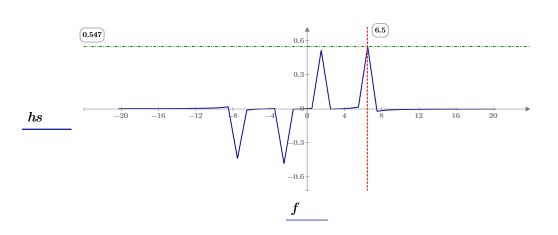
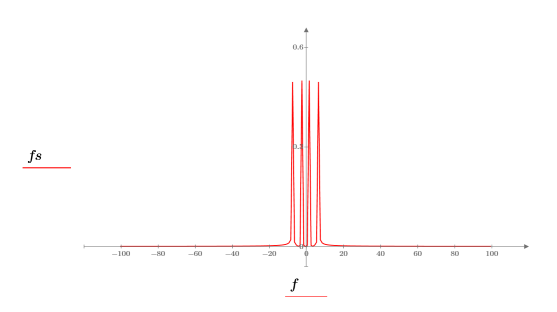
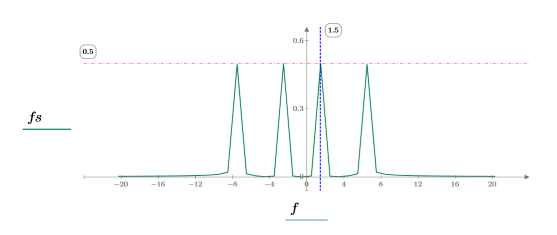
3. 繪製信號。
4. 使用
dht 函數顯示以兩個正弦波表示的離散頻率,然後使用
center 函數將 DC 元件移動至中心。
5. 使用
match 與
max 函數求解尖峰發生時的離散頻率,並透過垂直與水平標記將該點標示為 1。
6. 使用
dft 與
center 函數取得並置中離散傅立葉轉換。
7. 繪製 DFT 的絕對值。
8. 使用 match 與 max 函數求解出現尖峰時的離散頻率。
哈特利轉換與傅立葉轉換之間的密切關係,可透過顯示如何從哈特利轉換計算相角與量值來展現。使用小型的數據集即可達成。
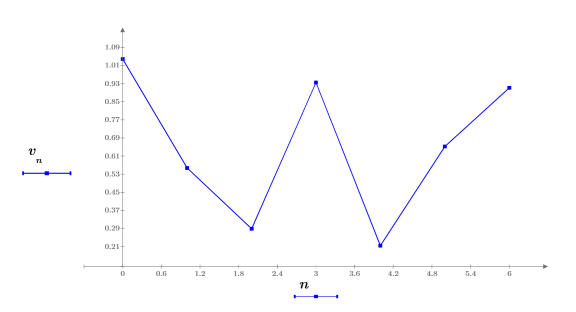
短雜訊信號
1. 定義及繪製 7 個樣本點的雜訊輸入信號。
2. 計算並置中離散哈特利轉換。
3. 計算離散哈特利轉換的奇數與偶數部份 (這些公式假設奇數值為 N)。
5. 定義量值向量。
7. 使用
augment 函數比較相角結果與透過傅立葉轉換獲得的結果。
相角結果相符。
8. 使用 dft 與 center 函數建立量值向量。
9. 使用 augment 函數比較量值結果與透過傅立葉轉換的結果。
量值結果相符。
如需哈特利轉換及其應用的完整論述,請參閱 Oxford University Press 發行由 Ronald Bracewell 所著的 The Hartley Transform (哈特利轉換)。