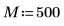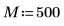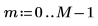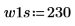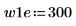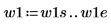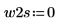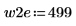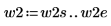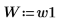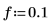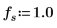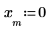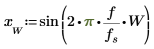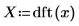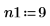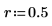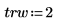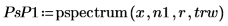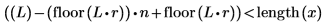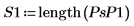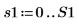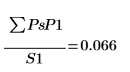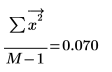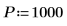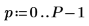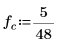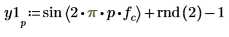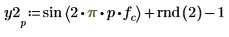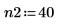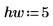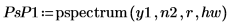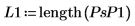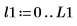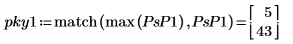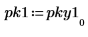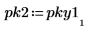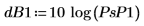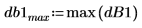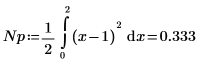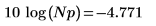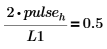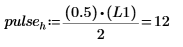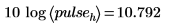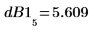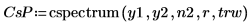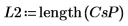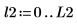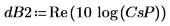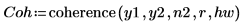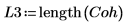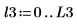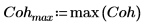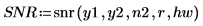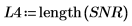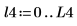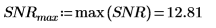範例:光譜分析
使用
coherence、cspectrum、pspectrum 與
snr 函數可計算信號或成對信號的連貫性、交叉頻譜、功率頻譜及「信號-雜訊」比。
如需有關此平均程序的描述,請參閱 Samuel Stearns 與 Ruth David (Prentice-Hall, Inc.) 提出的信號處理演算法。
功率頻譜 - 使用 DFT
若是很長的時間序列,其中僅有少數的數據點值與信號相對應,則功率頻譜最好是顯示信號的頻率,而不是雜訊或零值。
1. 定義視窗寬度。
2. 定義兩個可能的視窗 w1 與 w2,在這些視窗中信號不為零。
3. 將視窗寬度設為兩個可能寬度之一。
4. 定義信號與取樣頻率。
5. 使用
sin 函數定義所選視窗內部與外部的信號。
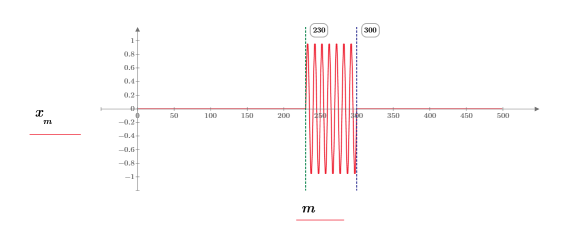
6. 繪製信號。
7. 使用
dft 函數,以計算
x 的離散傅立葉轉換。
8. 在頻域中繪製所得出的函數。
◦ 對於純正弦波信號,DFT 係數的量值有助於合理預估其功率頻譜。但在此情況下,信號的 DFT 是透過矩形窗 (
sinc 函數) 轉換迴旋積分之結構化信號的頻率內容。
◦ 設定 W= w2 (步驟 3) 可加寬在 230–300 與 0–499 之間存在正弦波信號 (係數 7.143x) 的視窗,結果會增加在 35 與 250 之間的兩個尖峰量值 (係數同樣為 7.143x)。
◦ 發生尖峰的頻率維持不變。
功率頻譜 - 使用 pspectrum
pspectrum 函數會將原始時間序列分為重疊的區段。DFT 會轉換每個區段,並對轉換量值的係數求平均值。若區段的長度與信號中要分析的現象使用相同的縮放,則 pspectrum 函數會適當傳回原始時間序列中較關注之部分元件量值的近似值。
一般而言,信號的長度至少應為 n + 1。
1. 定義信號長度、重疊分數和視窗類型 (矩形窗)。
2. 使用 pspectrum 函數計算 x 的功率頻譜,所採用的方式是使用重疊區段分數 r 將 x 分隔為 n1 重疊區段,並透過矩形窗為每個區段加窗。
4. 使用常態化頻率軸 (1 表示取樣頻率) 繪製頻譜。
5. 計算頻譜的平均乘冪。
這是信號 x 的均方近似值。
包含白雜訊的 pspectrum
計算包含白雜訊的信號功率頻譜。由於交叉頻譜計算需要第二個信號,因此請產生兩個此類信號。使用漢明窗取數據區塊窗。
1. 定義信號寬度。
2. 使用
sin 與
rnd 函數定義具有通用頻率
fc 的兩個信號。
rnd 函數會傳回在 0 與指定編號之間均等分佈的亂數的向量,進而確保信號保持在不同狀態。
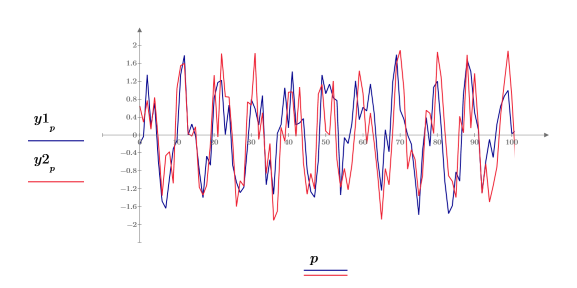
3. 繪製這兩個信號的前 100 個樣本。
4. 使用 pspectrum 函數獲取 y1 的功率頻譜,所採用的方式是使用重疊區段分數 0.5 將其分隔為 40 個重疊區段,並透過漢明窗為每個區段加窗。
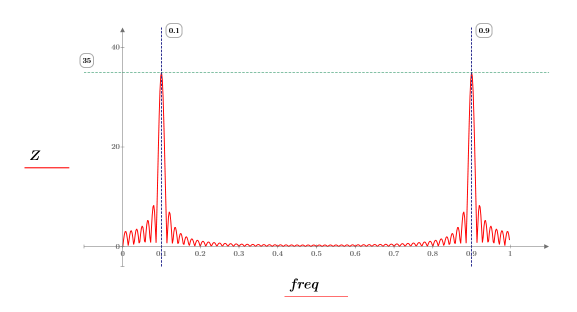
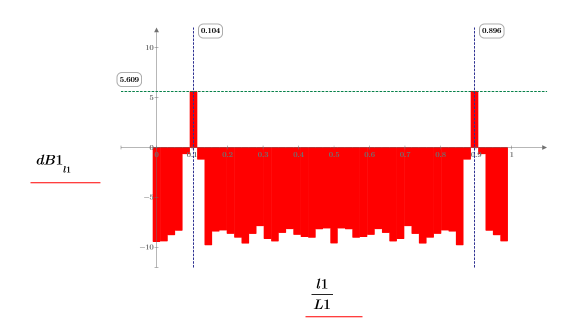
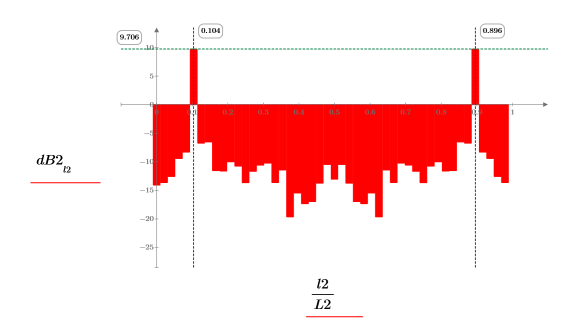
6. 繪製以分貝為單位的頻譜。使用標記標示一般頻率與最大分貝值。
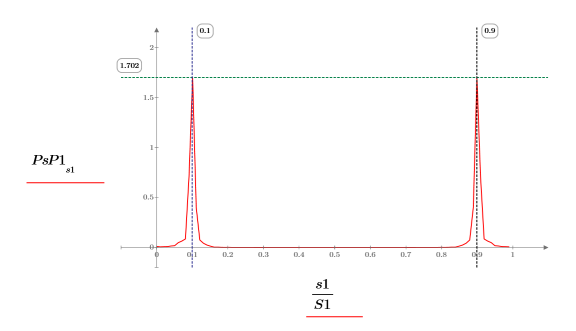
繪圖會顯示所有信號功率都發生在一般頻率 fc 與 1-fc。
7. 計算雜訊功率。
8. 計算雜訊功率增量 (以 dB 為單位)。
9. 高度計算所根據的事實,是將以上兩個頻率樣本除以頻譜長度應得到正弦元件的平均功率 (亦即 0.5)。
10. 以分貝為單位比較理論高度與實際高度。
cspectrum 函數
交叉頻譜通常用以檢測兩個信號的相似度,例如,比較已知語音信號波形 (如母音 a) 與未知語音信號波形 (如單字 apple),以判定未知信號波形中是否存在已知信號波形。就如同時間序列的功率頻譜類似其自相關運算一般,兩個時間序列的交叉頻譜也類似其交互相關運算。就靜態隨機序列而言,頻譜函數會傳回與相關函數相同的值。
1. 將 cspectrum 函數套用至信號 y1 與 y2,使用 40 個重疊分數為 0.5 的重疊區段,並以矩形窗顯示每個區段。
2. 繪製以分貝為單位的頻譜。
3. 繪製交叉頻譜;請注意,此頻譜為複數,因此應將對數應用至量值。
y1 與 y2 的交叉頻譜在一般頻率 fc 與 1- fc 時顯示尖峰。
coherence 與 snr 函數
coherence 函數會量測某信號對其他信號的線性依存度,並且等於以兩個功率頻譜分割的兩個信號之交叉頻譜的平方量值,值的範圍介於零與一之間。coherence 函數值為 1,通常表示這兩個信號在該頻帶中的元件沒有高雜訊,而值為 0 則表示在該頻帶中有最多雜訊。
「信號-雜訊比」snr 函數等於 coherence 函數除以一減去 coherence 函數;且當兩個信號在任何元件頻帶中有強元件時會是最大值,並會與信號強度對感應器或背景雜訊強度比成正比。
1. 將 coherence 函數套用至信號 y1 與 y2,使用 40 個重疊分數為 0.5 的重疊區段,並以漢明窗顯示每個區段。
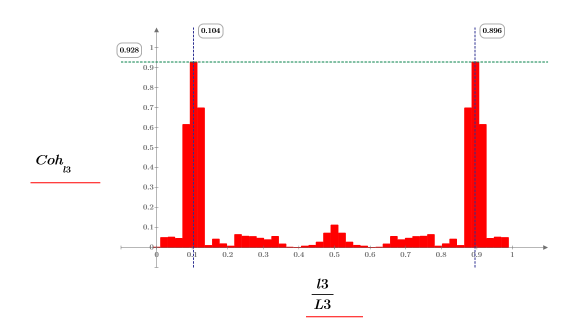
2. 繪製 coherence 函數。使用標記標示一般頻率與最大值。
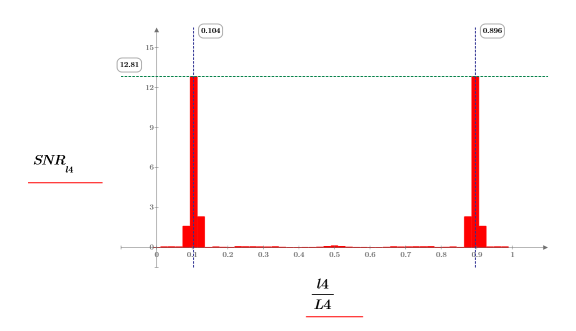
3. 將 snr 函數套用至信號 y1 與 y2,使用 40 個重疊分數為 0.5 的重疊區段,並以漢明窗顯示每個區段。
4. 繪製信號-雜訊比函數。使用標記標示一般頻率與最大值。
coherence 與 snr函數都會在兩個信號的單一頻率元件上顯示最大值,並在兩側以兩個較短的直條表示加入的雜訊。