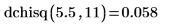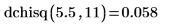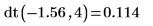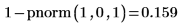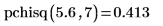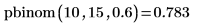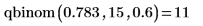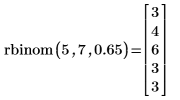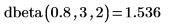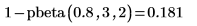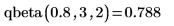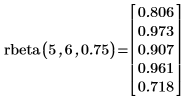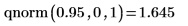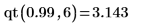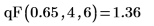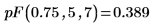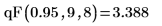範例:機率分佈
在機率分佈表中使用機率分佈函數。
機率密度
1. 使用
dchisq 函數計算自由度為 11 之 5.5 的卡方變數機率密度:
2. 使用
dt 函數計算自由度為 4 之 -1.56 的變數
t 機率密度:
累積機率
1. 使用
pnorm 函數計算標準常態變數超過 1.0 的機率:
2. 使用
pchisq 函數計算自由度為 7 之卡方變數小於 5.6 的機率:
3. 使用
pbinom 函數計算大小為 15 且參數為 0.6 的二項變數小於或等於 10 的機率。
4. 使用
qbinom 函數計算大小為 15 且參數為 0.6 的二項變數小於或等於 10 的機率。
5. 使用
rbinom 函數建立含有大小為
n=7 且成功機率為
q=0.65 之二項分佈的
m=5 亂數向量。
| 重新計算工作表會導致函數 rbinom 傳回一組新的亂數。 |
6. 使用
dbeta 函數,為實數形狀參數 3 與 2 計算值
x=0.8 的機率密度:
7. 使用
pbeta 函數計算 beta 變數 (
a=3 及
b=2) 超過 0.8 的機率:
8. 使用
qbeta 函數計算機率
p=0.8 的累積機率逆分佈:
9. 使用
rbeta 函數建立含有大小為
n=6 且成功機率為
q=0.75 之二項分佈的
m=5 亂數向量。
逆累積機率
1. 使用
qnorm 函數計算機率
p 的累積機率逆分佈:
2. 使用
qt 函數計算機率
p 的累積機率逆分佈:
F 分佈
1. 使用
dF 函數計算自由度為 4 與 6 之 F 分佈的第 65 個百分位數:
2. 使用
pF 函數計算自由度為 5 與 7 之機率 0.75 的累積機率分佈:
3. 使用
qF 函數計算自由度為 9 與 8 之 F 分佈的第 95 個百分位數:
4. 使用
rF 函數建立具有自由度為 2 與 3 之 F 分佈的 7 個亂數向量:
| 重新計算工作表會導致函數 rF 傳回一組新的亂數。 |