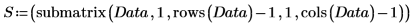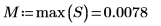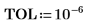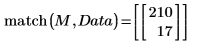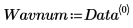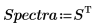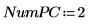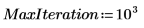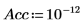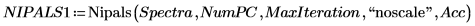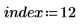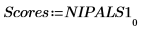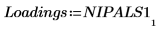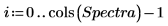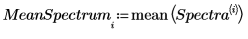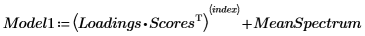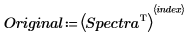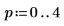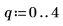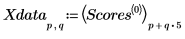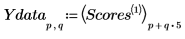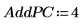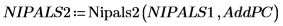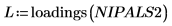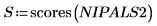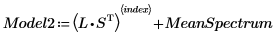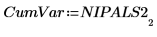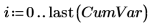範例:主元件分析 2
使用
Nipals 及
Nipals2 函數分析複數數據,例如藥片的近紅外線 (NIR) 頻譜與五種不同的實際原料投藥量 (Bruker Optics, Inc. 提供數據並授權使用)。即使不知道實際的投藥量,根據頻譜建立的模型仍可區別每次的投藥量。日後生產藥片時,此模型可用於品管目的。
1. 定義下列數據集:
第一欄為以 cm-1 表示的波數 (1/波長)。每個投藥量有 5 個連續頻譜,構成其餘 25 欄。
3. 使用
max 與
match 函數求解最大值及包含它的頻譜。由於數據值非常小,請將
TOL 設定為較小的偶數值。
最大值位於數據矩陣的 210 列與 17 欄中。
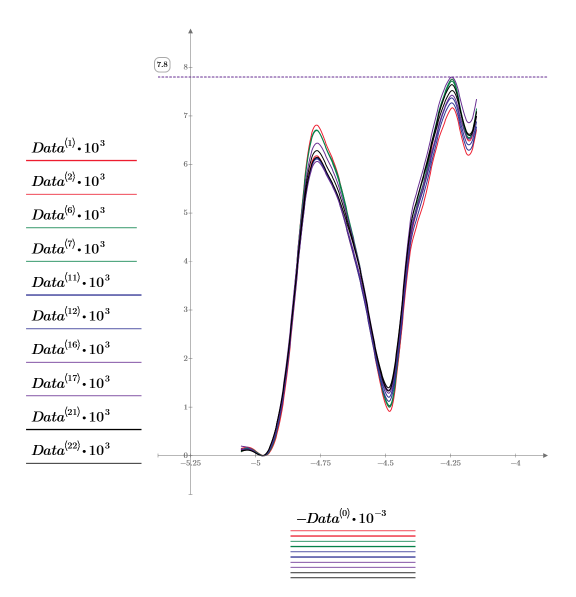
4. 繪製各投藥量的前面兩個頻譜,總計 10 個數據集。數據集對為 Data 矩陣的 [1,2]、[6,7]、[11,12]、[16,17] 與 [21,22] 欄。
◦ 若要取得水平軸的合理比例,請將波數除以 1000。同樣地,由於頻譜值較小,因此乘以 1000。
◦ 使用水平標記顯示最大頻譜值。
◦ 依慣例,波數會隨遞減順序繪製。Data<0> 會因此遭到取消,以便以正確的順序顯示波數。
◦ 頻譜的任何部份都無法用於輕鬆區別不同的投藥量︰它們全部都有相同的基本形式及近似的吸收值。
◦ 大部分的數據都是多餘的。每份頻譜有 236 個點,這表示 236 個量測的變數 (特定光波長的吸收率),但這些點的變化明顯相互關連。
5. 將 Data 矩陣分割成兩個數據集:每片藥的波數 (欄 0) 及頻譜 (子矩陣 S)。若要符合常見慣例,請轉置每片藥的頻譜,使各欄對應至自變數。
6. 將
Nipals 函數套用至數據之前,先定義主元件的數目,以及疊代的最大數目。
Nipals 函數會集中數據,減去各列的均數頻譜。
7. 選擇要重新建構的頻譜。
8. 從 Nipals 函數的輸出萃取分數及影響力。
9. 使用 mean 函數計算均數頻譜。
10. 將影響力向量矩陣乘以分數矩陣,再加上均數頻譜,即可得出原始頻譜的估值。
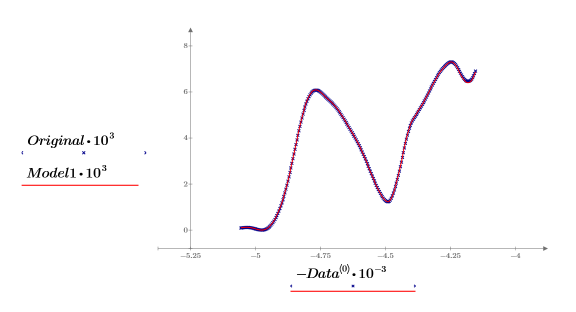
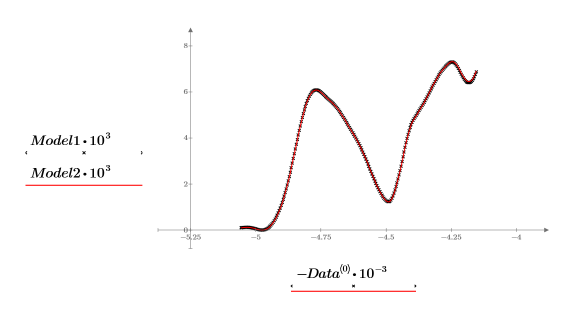
11. 繪製原始與重新建構的頻譜。縮放水平軸與垂直軸,以獲得合理值。
只要使用兩項主元件進行主元件分析,即可表示所有的頻譜。
12. 將分數重新排列到兩個矩陣。矩陣的每一欄代表五片投藥量其中之一的分數。
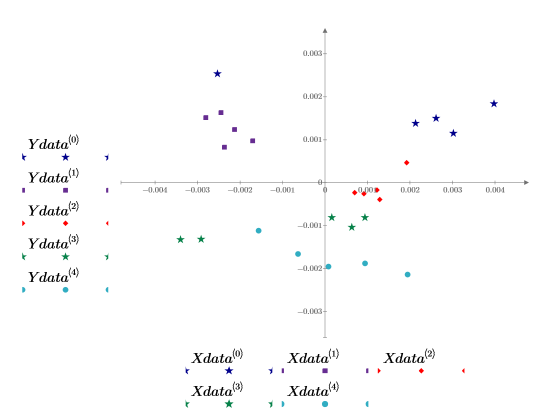
13. 對照第二係數的分數,繪製第一係數的分數。每種投藥量都以不同的顏色顯示。
某些數據的分組非常明顯,但仍難以區分不同的投藥量。將第三個分數新增至繪圖可能會有所幫助。
14. 使用 Nipals2 函數將 4 個主元件加入以 2 個主元件建立的模型。
NIPALS2 的輸出矩陣與 NIPALS 的格式相同,但有對應至其他主元件的其他欄與列。分數與影響力的數目現已增加至 6。
15. 從 NIPALS2 矩陣萃取影響力及分數,以建立所選頻譜的新模型。
16. 繪製並比較所選頻譜的這兩個模型。縮放水平軸與垂直軸,以獲得合理值。
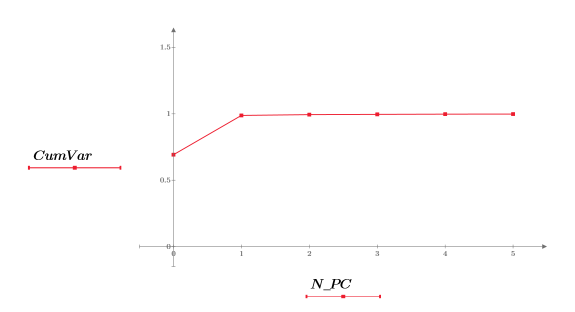
17. 從 NIPALS2 萃取累積變異數。
18. 對照主元件數,繪製累積變異數。
雖然前兩項主元件 (PC) 代表 99% 的變異數,但第三項 PC 才是依投藥量組合數據的關鍵。主元件分析會將數據壓縮為最具優勢的係數,但不是最相關的係數。