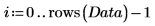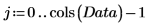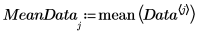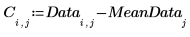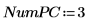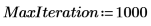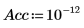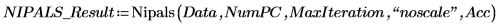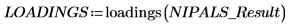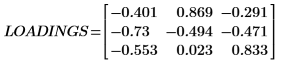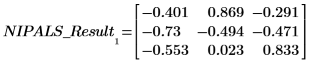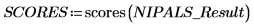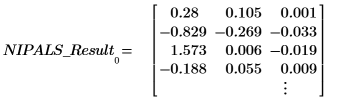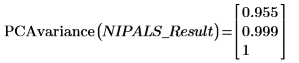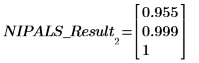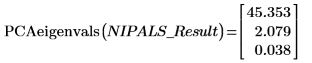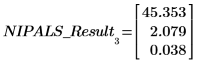範例:主元件分析 1
Nipals 函數
1. 定義每欄各代表一項變數的數據集。
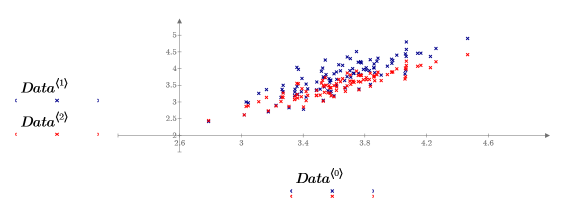
2. 繪製數據集。
在本圖表中,x-y 面與 x-z 面重疊以揭露數據的趨勢線。數據其實是幾乎全在一個平面上的楕圓形點雲。這三個變數都線性相關,完美平面的偏差都是因為雜訊所致。
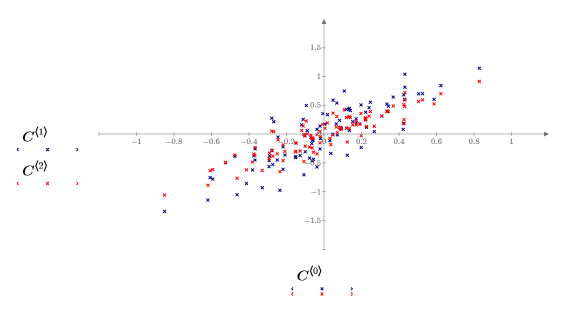
4. 使用均數函數求解數據的均數,然後減去每個變數的均數,以置中數據。
5. 繪製置中的數據。
| • 數據現已集中在原點周圍。此為 Nipals 函數自動運行的步驟之一。 • 在許多 PCA 應用中,也常會縮放數據讓變數有相同的權重,例如當不同的變數有不同的單位時。將各變數 (數據各欄) 縮放成單位變異數很常見,但不適用於此數據,所以此處未使用縮放。 |
6. 使用 Nipals 函數建立新的變數空間。使用 3 個主元件,此為可能的上限,因為一開始只有 3 個變數。
影響力與分數
1. 呼叫 loadings 函數以擷取在 NIPALS_Result 第二個矩陣中所求得的數據。
LOADINGS 的每一欄都是負載向量。
2. 呼叫 scores 函數以擷取在 NIPALS_Result 第一個矩陣中所求得的數據。
分數代表加上影響力向量以重建原始頻譜的比例。將其視之為強度。數據 = LOADINGS * SCOREST。
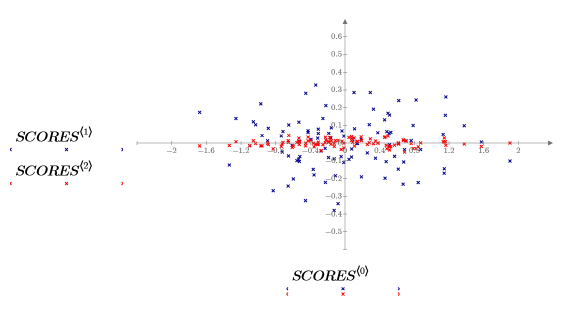
3. 繪製儲存在 SCORES 矩陣中的數據。
已旋轉數據,所以第一個變數可以說明最大量的變異數。表現在圖表上是橢圓形雲的長軸,現與 x 軸平行。與 z 軸平行的第三個變數的值非常小。此變數在大多數的用途中可予以忽略。您已壓縮數據。
PCA 變異數與本徵值
前兩個元件會製造方程組中 99.9% 的變異數。