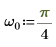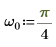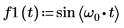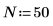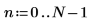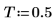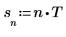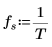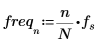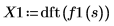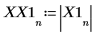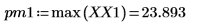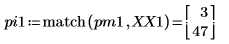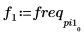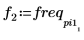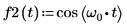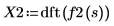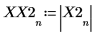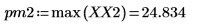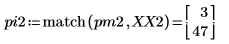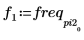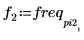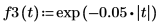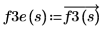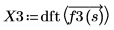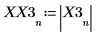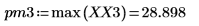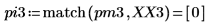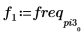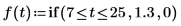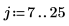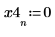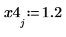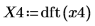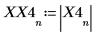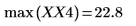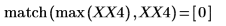範例:介紹 FFT
快速傅立葉轉換 (FFT) 是一種表示量測過一段時間之數據集頻率內容的數值方法。數據通常是連續的,會構成波形。若要以數值方式處理數據,要按某種取樣率以規律的時間區間取樣。以下各圖說明某些取樣的波形,及其針對頻率所繪製的傅立葉轉換量值。
取樣的正弦波形
2. 設定數據點數目。
3. 設定樣本間距。
4. 設定取樣比率。
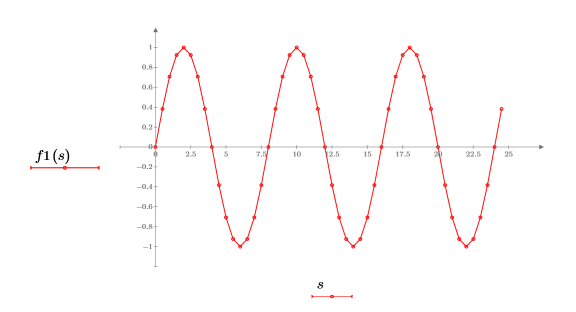
5. 繪製正弦曲線函數。
X1 是實數和複數的向量。
7. 求解出現尖峰量值的頻率。
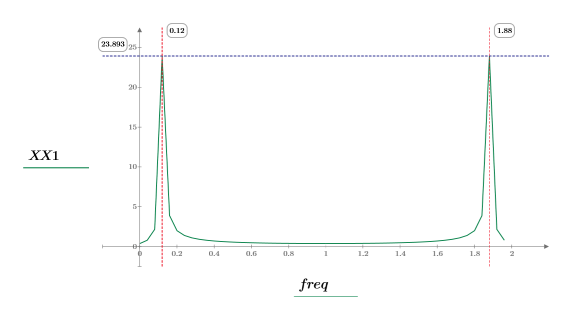
8. 繪製轉換信號,並使用標記顯示尖峰的頻率與量值。
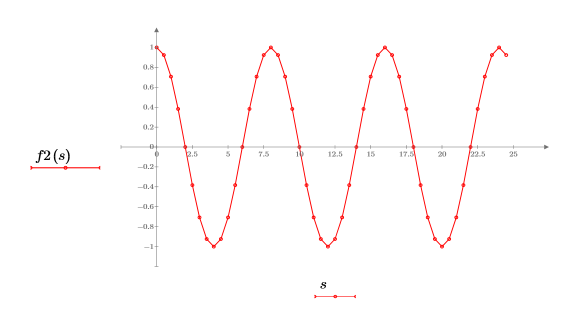
取樣的餘弦波形
2. 繪製餘弦函數。
3. 使用 dft 函數計算離散傅立葉轉換。
X2 是實數和複數的向量。
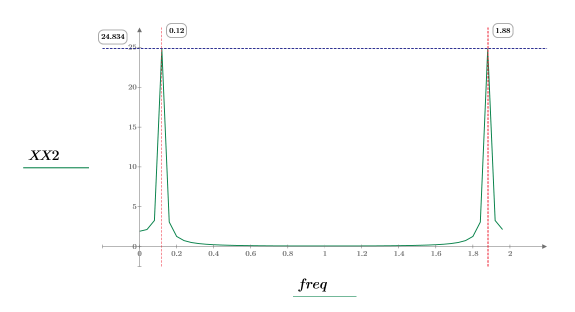
4. 求解出現最大量值的頻率。
5. 繪製轉換信號,並使用標記顯示尖峰的頻率與量值。
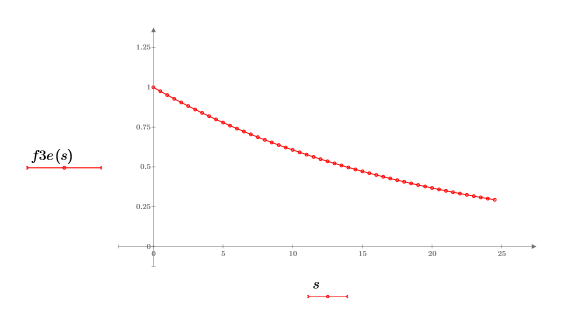
取樣的指數波形
向量化運算子可用於取得函數的逐元素值,因為定義內的行列式運算子會傳回單一純量值。
2. 繪製正弦曲線函數。
3. 使用 dft 函數,以計算離散傅立葉轉換。
X3 是實數和複數的向量。
4. 求解出現最大量值的頻率。
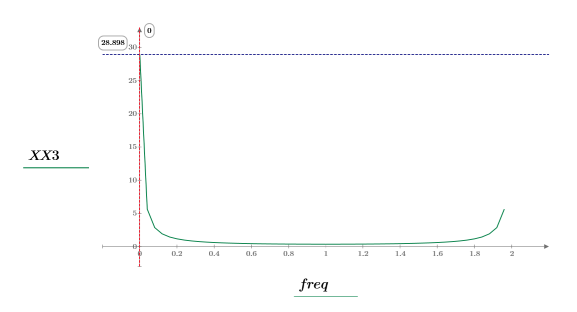
5. 繪製轉換信號,並使用標記顯示尖峰的頻率與量值。
取樣的階梯波形
2. 計算每個區間的脈衝量值。
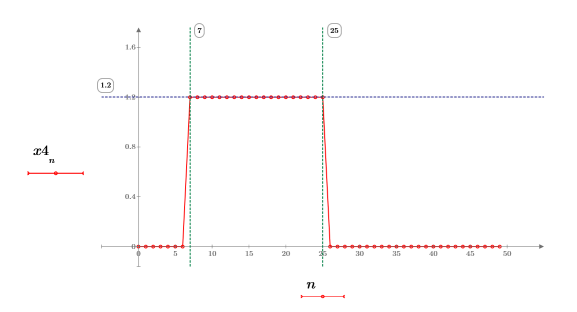
3. 繪製階梯函數。
量值一致且等於 1.2,介於 7 及 25 之間。
4. 使用 dft 函數,以計算離散傅立葉轉換。
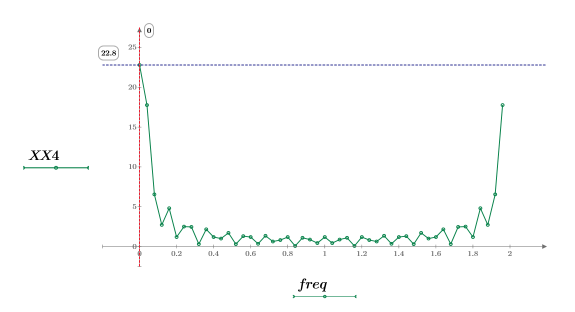
X4 是實數和複數的向量。
5. 求解出現最大量值的頻率。
6. 繪製轉換信號,並使用標記顯示尖峰的頻率與量值。
最大量值發生於 freq0。