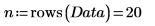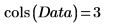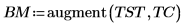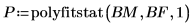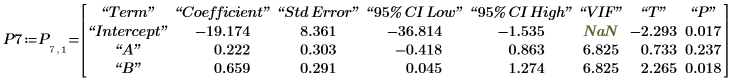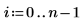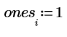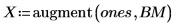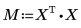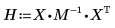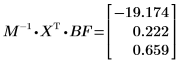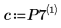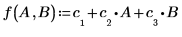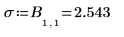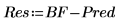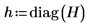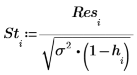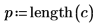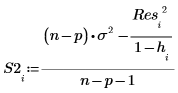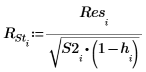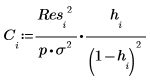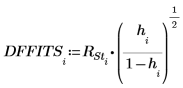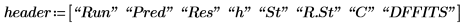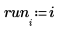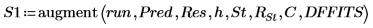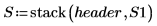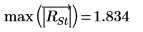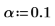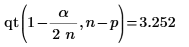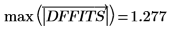範例:找出具影響力的觀測值
使用函數
polyfitstat 檢驗建立多變量多項式遞歸所用的觀測。
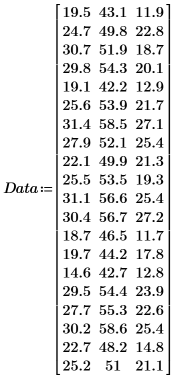
1. 定義包含取樣自 20 名 25 歲到 34 歲身體健康之個人的矩陣。
矩陣的欄分別代表 20 個人每位的三頭肌皮下脂肪厚度、大腿圍及體脂肪。
3. 使用
augment 函數將矩陣
BM 定義為矩陣的前兩欄。使用這些量測預測每個人的脂肪量。
4. 呼叫 polyfitstat 由第一階遞歸建立實驗模型,並計算遞歸統計。
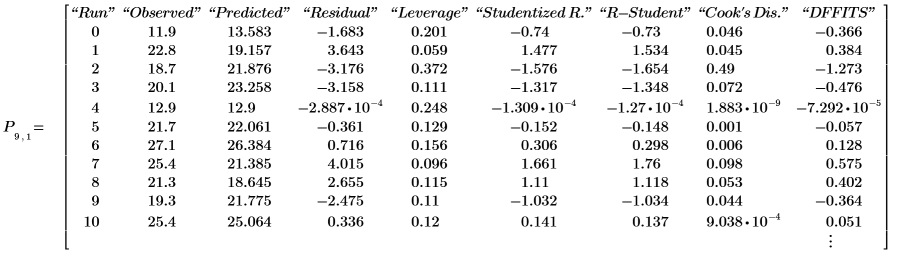
5. 顯示在輸出矩陣 P 的列 7 中找到的遞歸係數矩陣。
6. 使用矩陣計算來計算遞歸係數。
遞歸係數可擬合下列方程式:
7. 使用遞歸方程式計算預測的體脂肪量。比較這些值與量測到的體脂肪量。
8. 使用 submatrix 函數顯示在輸出矩陣 P 的前幾列中找到的模型統計。
第一項統計是遞歸標準差。
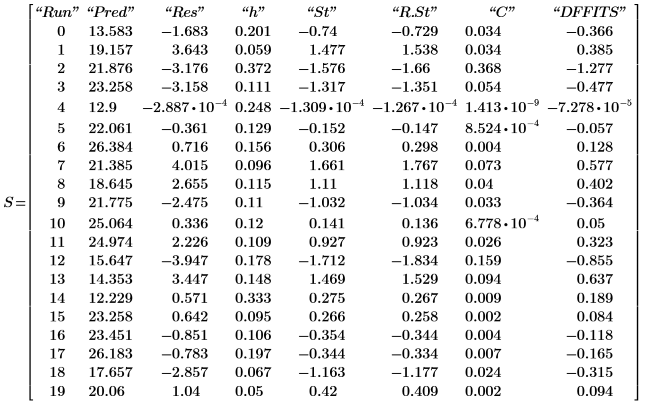
9. 顯示在輸出矩陣 P 的最後一個巢狀矩陣中找到的模式診斷。
與步驟 7 中所顯示的值相對應之觀測值及預測值。殘差為觀測值與預測值之間的差分:
10. 計算殘差 (或觀測值與預測值之間的差分)。
11. 使用函數
diag 計算矩陣
H 的槓桿效率值 (或對角值)。
12. 計算 T 化殘差。
在外部進行 T-測試的殘差或 R-student 計算如下。常數 p 是遞歸計算的係數數目,而 S2 是以移除了第 i 項觀測之數據集為基礎的 s2 預估值。
13. 使用庫克距離量測已刪除點對線性遞歸的整體影響。
14. 計算當擬合中包含所有觀測時的預測值差分,以及省略第 i 項觀測時的預測值差分。
15. 使用函數
augment 與
stack 顯示上述統計。
16. 使用函數
max 與
qt 判斷數據集中最大的 R-student 值。使用 Bonferroni 檢驗決定對應觀測是否為離群值。
最大的 R-student 值小於 Bonferroni 檢驗,而後者指出對應的觀測不是離群值。
17. 判斷最大的 DFFITS 值。
此值大於 1 但近似於 1,因此對應的觀測非必要影響。
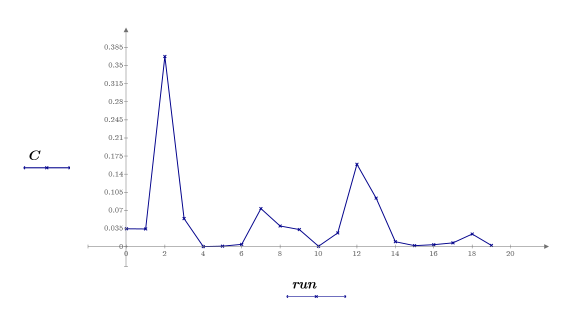
18. 針對執行繪製庫克距離,以建立索引影響圖。
run2 觀測是最具有影響力的數據集觀測。在步驟 10 中識別的 run12 觀測也具有影響力,但對 run2 的影響力較小。
參照
參照:Neter, J., Kutner, M.H., Nachtsheim, C.J., Wasserman, W., Applied Linear Statistical Models, 4th ed., McGraw-Hill/Irwin, Boston, 1996, pp.375