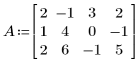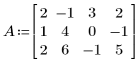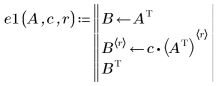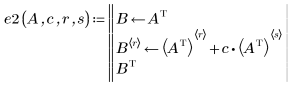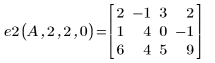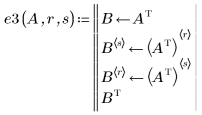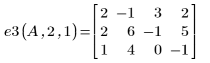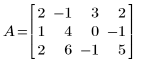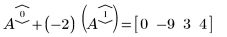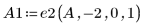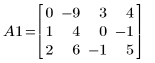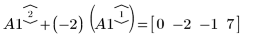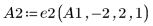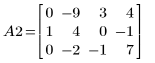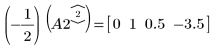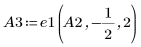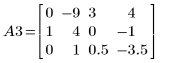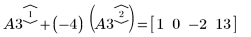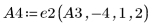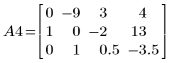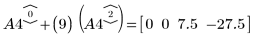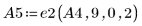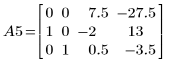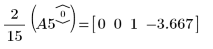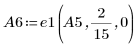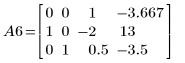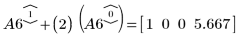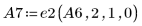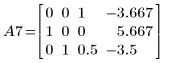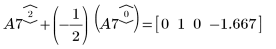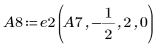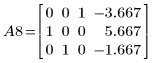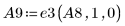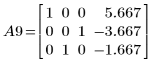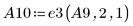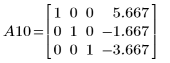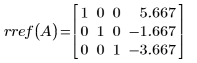範例:矩陣上的基本列運算
對 m x n 矩陣執行三種基本列運算類型,並顯示具有列簡化梯形式的連接。
1. 定義輸入矩陣:
2. 將列 r 乘以純量 c:
3. 將列 r 取代為列 r 加 c 乘以列 s:
4. 將列 r 與 s 互換:
矩陣的列簡化梯形式 (rref)
列簡化梯形式是用以求解線性方程式系統的重要技術。
利用以下 e1、e2 及 e3 運算順序,求解矩陣 A 的列簡化梯形式 (rref):
1. 定義矩陣 A
2. 使用 e2 將 A 的列 0 取代為列 0 加 (-2) 乘以列 1:
3. 使用 e2 將 A1 的列 2 取代為列 2 加 (-2) 乘以列 1:
4. 使用 e1 將 A2 的列 2 乘以 (-1/2):
5. 使用 e2 將 A3 的列 1 取代為列 1 加 (-4) 乘以列 2:
6. 使用 e2 將 A4 的列 0 取代為列 0 加 (9) 乘以列 2:
7. 使用 e1 將 A5 的列 0 乘以 2/15:
8. 使用 e2 將 A6 的列 1 取代為列 1 加 (2) 乘以列 0:
9. 使用 e2 將 A7 的列 2 取代為列 2 加 (-1/2) 乘以列 0:
10. 使用 e3 將列 0 與 A8 的 1 互換:
11. 使用 e3 將列 1 與 A9 的 2 互換:
在此範例中,以上基本列運算順序會指定矩陣 A 的列簡化梯形式。
12. 使用
rref 函數求解矩陣
A 的列簡化梯形式。
傳回的矩陣與矩陣 A10 相同。