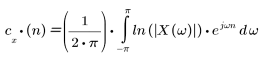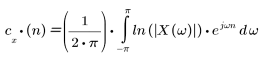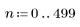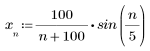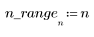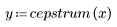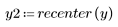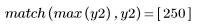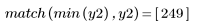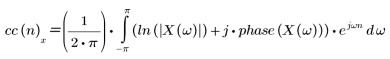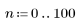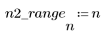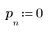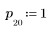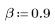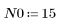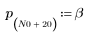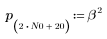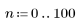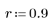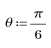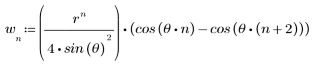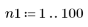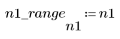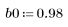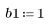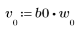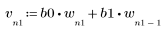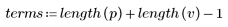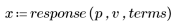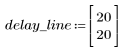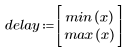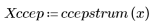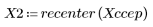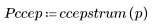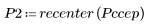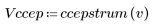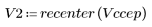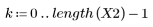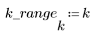範例:倒譜與複倒譜
使用
cepstrum 與
ccepstrum 函數計算實數多頻道信號的倒譜與複倒譜。
cepstrum 會將迴旋積分與反摺積對映至頻域中的加法與減法,並應用至語音及地球物理學信號處理。
cepstrum
下列方程式指定序列 x(n) 的倒譜:
其中 X(ω) 是序列 x(n) 的傅立葉轉換。
此為將自然對數套用至 x(n) 的傅立葉轉換之後的逆轉換定義。該對數會將時域中的迴旋積分對映至頻域中的加法,使 cepstrum 成為執行信號反摺積 (對映至減法) 的便利工具。
1. 定義 n 的值域。
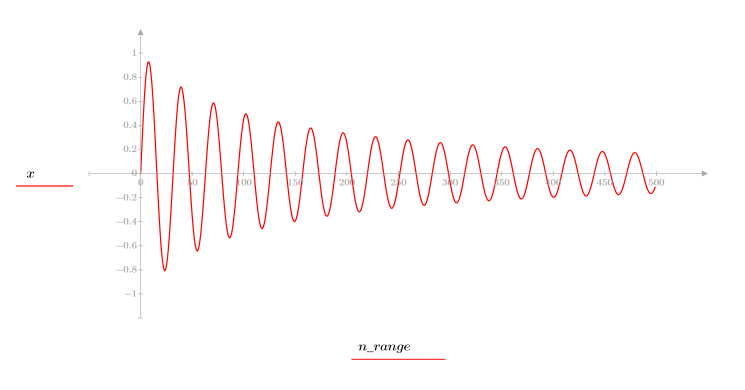
2. 定義序列函數 x。
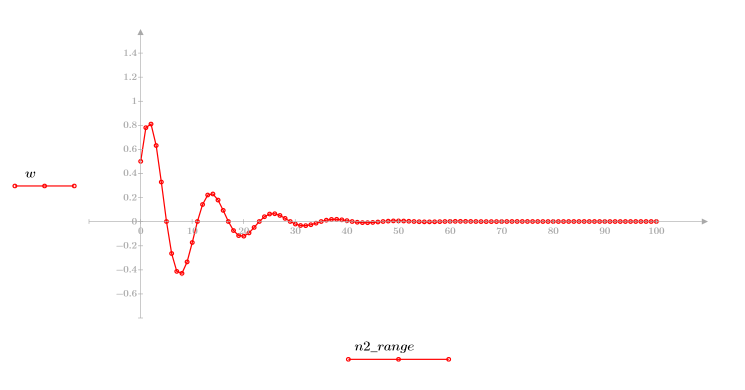
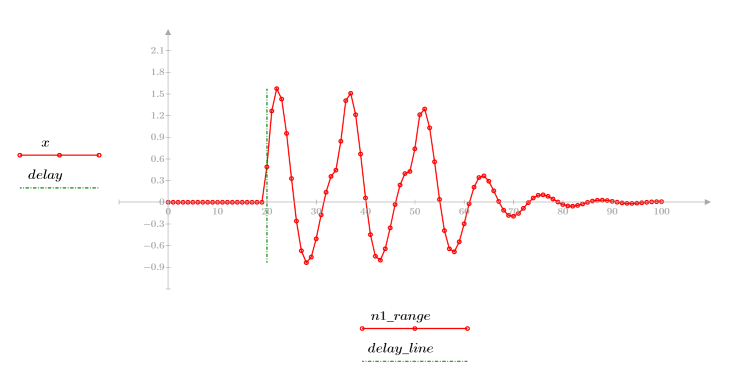
3. 繪製序列函數 x。
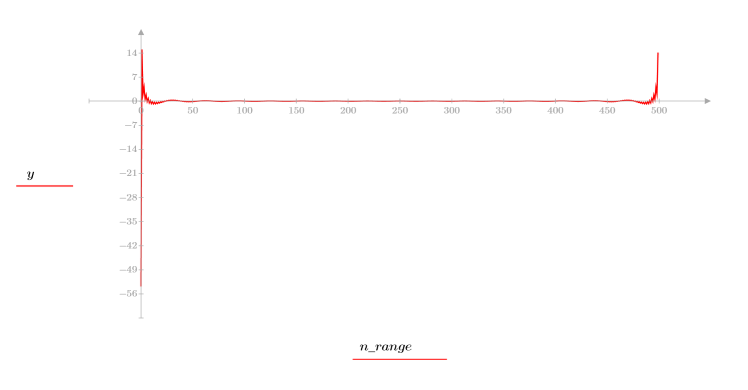
4. 計算 cepstrum 並繪製所得出的函數。
無法從倒譜恢復原始信號,因為並未保留相角資訊。
ccepstrum
以下複數對數指定複倒譜函數。
其中:X(ω) 是序列 x(n) 的傅立葉轉換,而相角是用以擷取指定序列的相角資訊。
比較輸出信號的 ccepstrum 與輸入及頻道序列的 ccepstrum,即可看出輸出的 ccepstrum 是輸入與頻道的 ccepstrum 總和。此類似於在頻域中加入兩個信號的頻譜,但卻在時域中完成。
下列範例模擬信號通過通訊頻道,引入回波 (請參閱 Oppenheim and Schaefer, Prentice-Hall, 1989 的第 12.8.1 節)。
1. 將頻道回應定義並繪製為 FIR 濾波器,以引入其他序列的衰減複本 (回波)。
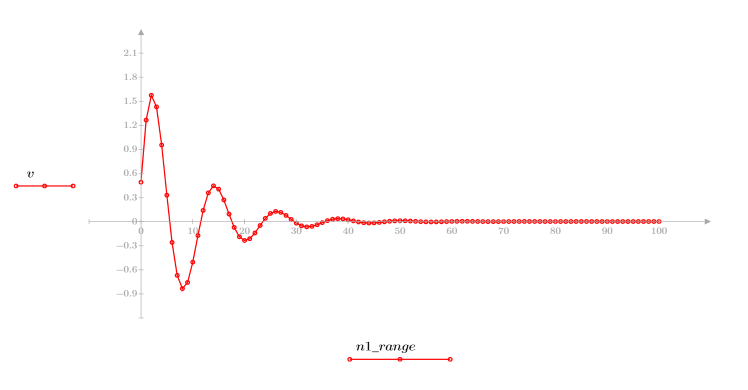
2. 定義並繪製將使用頻道回應迴旋的序列 v。
3. 使用
response 函數取得輸入向量 p 的 n 項向量回應,並送至含有係數陣列 v (通訊頻道函數 v) 的 FIR 濾波器。
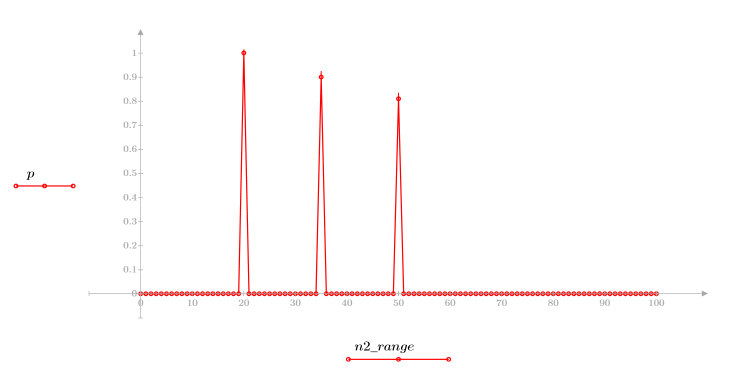
4. 繪製 response 函數。
◦ 產生的序列是輸入函數 p 與通訊頻道函數 v 的迴旋積分。
◦ 此序列顯示原始信號加上延遲的複本。
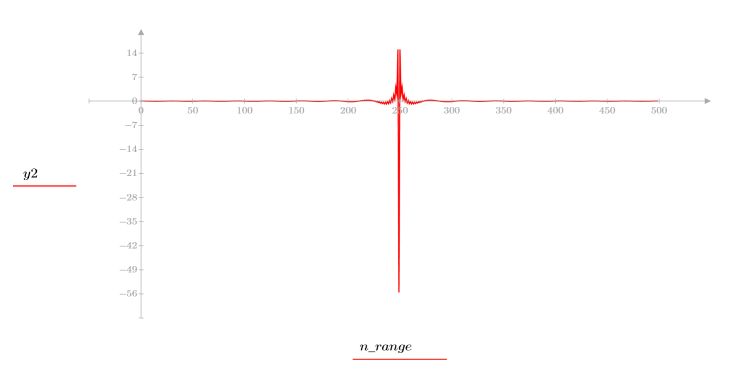
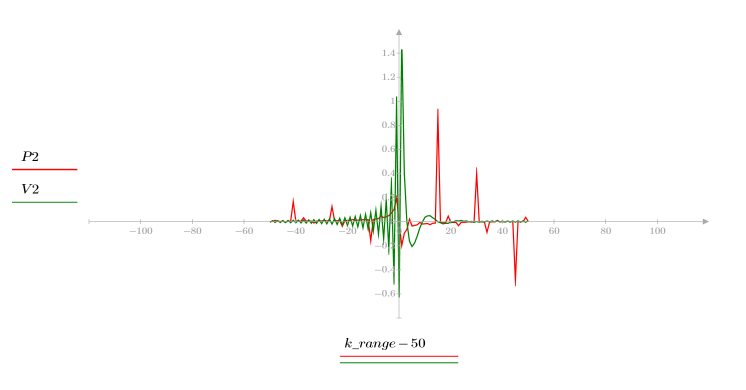
5. 比較輸出信號的複倒頻與原始序列的 cepstra。重新置中結果有助於進行比較。
以上繪圖顯示輸出信號的 ccepstrum 是兩個序列彼此迴旋的複數 cepstra 總和。