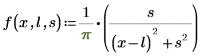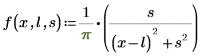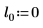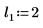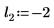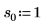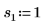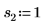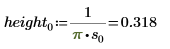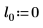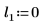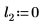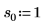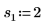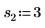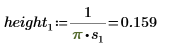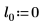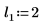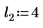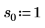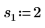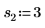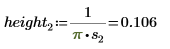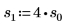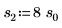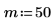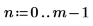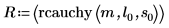範例:科西分佈
1. 顯示科西分佈的定義:
其中:
◦ l 是位置參數 (均數)
◦ s 是縮放參數 (變異數的平方根),s > 0
2. 定義三組位置與縮放參數,然後計算位置參數為 l0 且縮放參數為 s0 之曲線的振幅 (或高度):
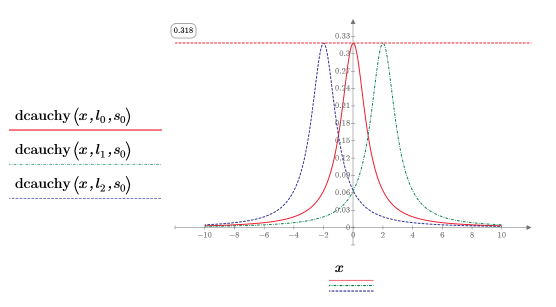
3. 使用
dcauchy 函數並搭配不同的位置參數值與固定的縮放參數,取得值
x 的機率密度:
不同的位置參數值會將曲線沿著 x 軸位移。
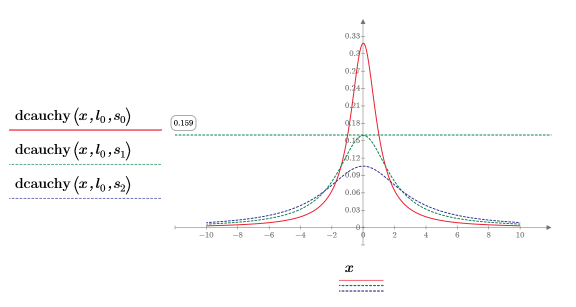
4. 使用固定的位置參數與不同的縮放參數值繪製 dcauchy 函數:
不同的縮放參數值會變更曲線的高度。
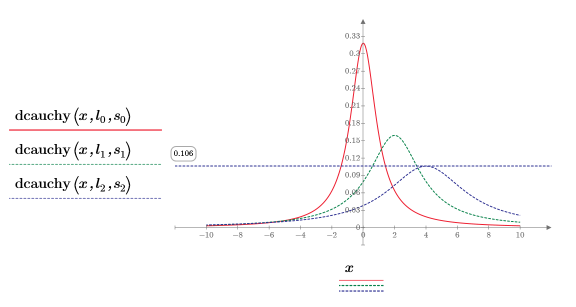
5. 使用不同的位置參數與縮放參數值繪製 dcauchy 函數:
不同的縮放與位置參數值會位移曲線並變更其高度。
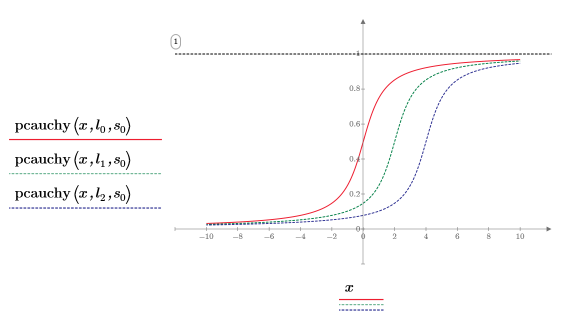
6. 使用不同的位置參數值與固定的縮放參數繪製
pcauchy 函數:
◦ 不同的位置參數值會將曲線沿著 x 軸位移。
◦ pcauchy 的所有 y 值介於 0 與 1 之間。
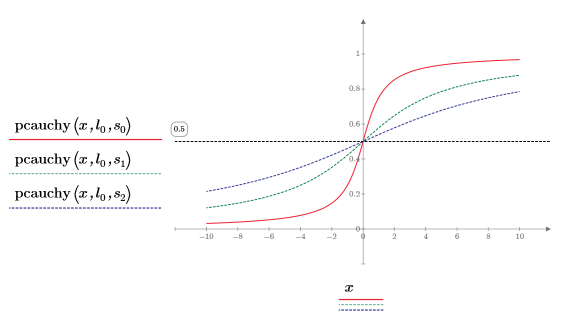
7. 使用固定的位置參數與不同的縮放參數值繪製 pcauchy 函數:
◦ 不同的縮放參數值會依水平方向展平曲線,但所有曲線會於 y=0.5 交會。
◦ pcauchy 的所有 y 值落在 0 與 1 之間。
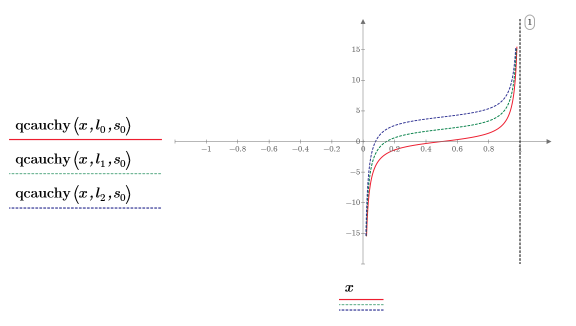
8. 使用不同的位置參數值與固定的縮放參數繪製
qcauchy 函數:
◦ 不同的位置參數值會將曲線沿著 y 軸位移。
◦ qcauchy 的所有 x 值落在 0 與 1 之間。
函數 rcauchy 傳回含有科西分佈的 m 亂數向量。
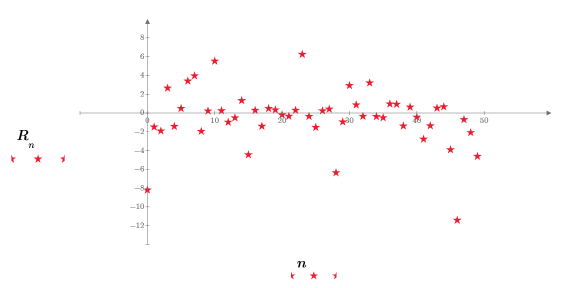
10. 繪製 rcauchy 函數傳回的亂數。
重新計算工作表會導致函數 rcauchy 傳回一組新的亂數,繪圖也會隨之更新。