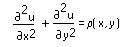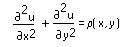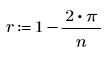PDE 的松弛法
• relax(A, B, C, D, E, S, U, rjac)
• multigrid(M, ncycle)
返回一个方阵,矩阵元素在其中所处的位置与其在方形区域中的位置相对应,且元素的值近似等于“泊松偏微分方程”(PDE) 的解
在该点的解。relax 函数采用修正的网格连续超松弛 Gauss-Seidel 方法求解泊松方程。
multigrid 函数采用 multigrid 方法,求解 U 中所有边界条件均为零的特殊情况。
• 如果边界条件为在四条边上均相等的常数,则应将方程变换为所有边均只含零边界条件并使用 multigrid,从而使设置更为迅速和便捷。
• 如果 ρ = 0,泊松方程可简化为拉普拉斯方程。
• 如果正在尝试求解双曲线 PDE 或抛物线 PDE,或是 PDE 方程组,则请使用 numol。
自变量
• A, B, C, D, E 为大小相同的实数方阵,它们包含函数 u 在四个最近邻点及近似点的离散拉普拉斯近似系数。
• S 是包含方阵中各点的源项的方阵。
• U 是包含区域边缘边界值及区域内部解的初始估值的方阵。
• rjac 是表示雅可比迭代谱半径的实数值 0 < rjac < 1。它控制松弛算法的收敛度。
rjac 的最优值取决于问题的详细信息,但 r 是一个理想的起始值,其中 n 为网格中每个方向的点数:
• M 是一个 1 + 2n 的方阵,其元素对应于方域中对应点处的源项。
• ncycle 是各级 multigrid 迭代的整循环次数。
通常,ncycle 值为 2 时可得到理想的近似解。