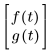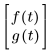ODE 関数
• odesolve(vf, b, [intvls]) - 初期値制約条件と境界値制約条件を満たす連立常微分方程式 (ODE) の解を表す関数を定義します。常微分方程式は、最高次の導関数項が線形であり、初期値制約条件と境界値制約条件の数が常微分方程式の階数と同じでなければなりません。
引数
• vf はソルブブロック内で使用される場合は関数または関数の列ベクトルです。
vf で関数を定義する場合、引数リストを指定する必要があります。たとえば、関数 f(t) と g(t) について解く場合、vf は次のように入力します。
• b は積分区間の終点を示す実数です。b は、ソルブブロック内で定義されている初期値より大きくても小さくても構いません。
• intvls (オプション) は、解の関数を補間するときに使用する離散化間隔の数を示す整数です。間隔の数に 1 を加えた数が解の点の数になります。intvls のデフォルト値は 1000 です。
通常、補間によって正確な解を得るのに intvls はデフォルト値で十分ですが、この値を大きくすることで、より精細な解を求めることもできます。値を大きくすると補間点が増えるため、odesolve による計算時間が長くなる場合があります。
大きな区間で常微分方程式の解を求める場合、intvls をデフォルトよりも大きい値に設定します。
その他の情報
• 関数 odesolve はソルブブロック内でのみ使用できます。
• レガシーの PTC Mathcad の関数 Odesolve はこれを小文字にしたものと交換できます。
• リボンから小文字の関数を挿入するか、小文字/大文字の関数を手入力すると、それに自動的に「キーワード」ラベルが割り当てられます。
• odesolve 関数は Adams/BDF 求解アルゴリズムを使用します。
• ソルブブロック内では、odesolve は TOL の値の影響を受けません。