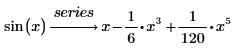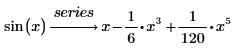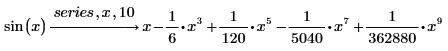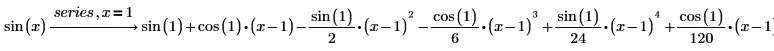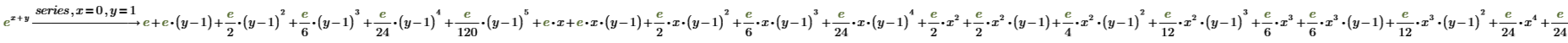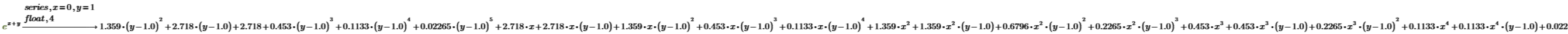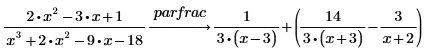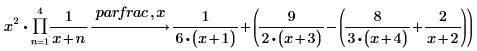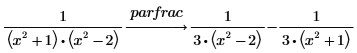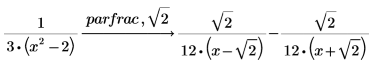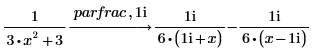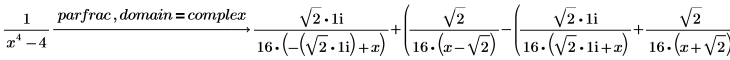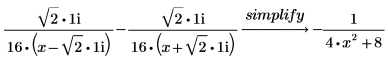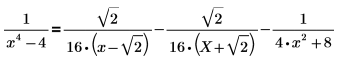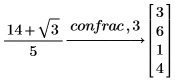例: シンボリックな微積分 2
シンボリック評価演算子を使用し、必要に応じてキーワードを追加して問題を変換して式を評価することにより、シンボリックな微積分問題を解きます。
テイラー級数とマクローリン級数
1. キーワード
series を使用して、
sin関数をマクローリン級数に展開します。
| デフォルトで、PTC Mathcad は 6 次までの項を返すので、解に含まれるべき数の最大は 5 になります。 |
2. series の後ろにコンマを入力し、プレースホルダーに x, 10 と入力して項の次数を 10 に増やします。
3. sin 関数を 1 についてのテイラー級数に展開します。
4. 複数の変数を持つ関数を点 (x, y)=(0, 1) において展開します。
5. 係数を e を使用してではなく 4 桁の数として表示します。
部分分数
1. キーワード parfrac を使用して、有理関数 (多項式の商) を部分分数へ変換します。
2. 範囲積演算子で定義された関数の部分分数分解を実行します。
実数または複素数への分解
デフォルトで、PTC Mathcad は有理数体について部分分数分解を実行します。つまり、最初の式が有理係数を持つ多項式の商である場合、結果の多項式にも有理係数が含まれます。
1. キーワード parfrac を使用して、次の関数を部分分数に分解します。
2. 次の式の項の 1 つをさらに分解します。
3. 有理関数を複素数まで完全に部分分数分解するには、parfrac の後に domain = complex を入力します。
| 実数まで分解するには、次の手順を実行します。 a. 次のようにキーワード simplify を使用して、最後の 2 つの項を結合して実数係数を持つ 1 つの項にします。 b. 元の結果を簡素化した結果に置き換えると、次のようになります。 |
連分数
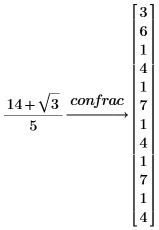
1. キーワード confrac を使用して、数値を連分数展開します。
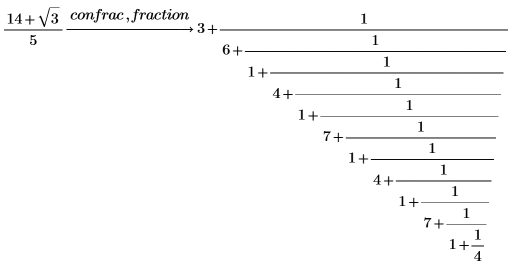
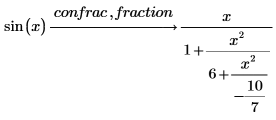
2. 変更因子 fraction を使用して、ベクトルではなく実際の連分数を表示します。
| PTC Mathcad では、デフォルトで十分に連分数展開された項が返るので、解は有効桁数 10 桁の精度を持ちます。 |
3. 有効桁数を指定する正の整数を追加すると、異なる精度の値が返ります。
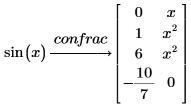
4. sin 関数を連分数として展開します。
| PTC Mathcad は、項に対応する x のべき乗を含む 2 列目を返します。 |