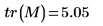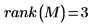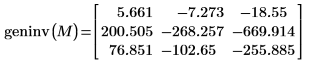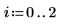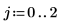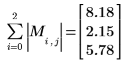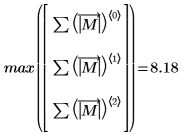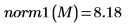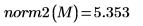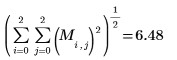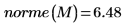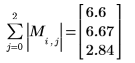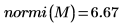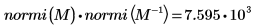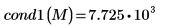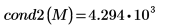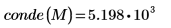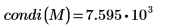例: 行列の特性

ベクトル、行列、テーブル > 配列の使用 > 例: 行列の特性

例: 行列の特性

正方行列のトレース、ランク、一般化逆行列、ノルム、条件数を求めます。

クリックしてこの式をコピー

トレース、ランク、および一般化逆行列

1. tr関数を使用してトレース、つまり M の対角成分の和を求めます。

クリックしてこの式をコピー

2. rank関数を使用して、実数値行列 M のランクを求めます。

クリックしてこの式をコピー

3. geninv関数を使用して行列 M の一般化逆行列を求めます。

クリックしてこの式をコピー

さまざまな行列のノルム

1. M のノルム L1 を求め、結果を関数 norm1の出力と比較します。

L1 ノルムは列の絶対値和の最大値です (j= 0, 1, 2 の中の最大値)。

クリックしてこの式をコピー

クリックしてこの式をコピー

クリックしてこの式をコピー

<region id="ID0EIJZOB" top="902.40000000000009" left="19.200000000000003" xml:lang="ja" height="62.800000000000004" width="134.8366666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="51" xml:lang="ja">
    <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <apply xml:lang="ja">
        <summation xml:lang="ja" />
        <lambda xml:lang="ja">
          <boundVars xml:lang="ja">
            <id xml:space="preserve" xml:lang="ja">i</id>
          </boundVars>
          <apply xml:lang="ja">
            <absval xml:lang="ja" />
            <apply xml:lang="ja">
              <indexer xml:lang="ja" />
              <id xml:space="preserve" xml:lang="ja">M</id>
              <sequence xml:lang="ja">
                <id xml:space="preserve" xml:lang="ja">i</id>
                <id xml:space="preserve" xml:lang="ja">j</id>
              </sequence>
            </apply>
          </apply>
        </lambda>
        <lowerBound xml:lang="ja">
          <real xml:lang="ja">0</real>
        </lowerBound>
        <upperBound xml:lang="ja">
          <real xml:lang="ja">2</real>
        </upperBound>
      </apply>
      <unitOverride xml:lang="ja">
        <placeholder xml:lang="ja" />
      </unitOverride>
    </eval>
  </math>
</region>

クリックしてこの式をコピー

<region id="ID0E1JZOB" top="1056.0000000000002" left="19.200000000000003" xml:lang="ja" height="136.00000000000003" width="191.66000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="53" xml:lang="ja">
    <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <apply xml:lang="ja">
        <id xml:space="preserve" xml:lang="ja">max</id>
        <matrix rows="3" cols="1" xml:lang="ja">
          <apply xml:lang="ja">
            <summation xml:lang="ja" />
            <lambda xml:lang="ja">
              <boundVars xml:lang="ja">
                <placeholder xml:lang="ja" />
              </boundVars>
              <apply xml:lang="ja">
                <matcol xml:lang="ja" />
                <parens xml:lang="ja">
                  <apply xml:lang="ja">
                    <vectorize xml:lang="ja" />
                    <apply xml:lang="ja">
                      <absval xml:lang="ja" />
                      <id xml:space="preserve" xml:lang="ja">M</id>
                    </apply>
                  </apply>
                </parens>
                <real xml:lang="ja">0</real>
              </apply>
            </lambda>
            <upperBound xml:lang="ja">
              <placeholder xml:lang="ja" />
            </upperBound>
          </apply>
          <apply xml:lang="ja">
            <summation xml:lang="ja" />
            <lambda xml:lang="ja">
              <boundVars xml:lang="ja">
                <placeholder xml:lang="ja" />
              </boundVars>
              <apply xml:lang="ja">
                <matcol xml:lang="ja" />
                <parens xml:lang="ja">
                  <apply xml:lang="ja">
                    <vectorize xml:lang="ja" />
                    <apply xml:lang="ja">
                      <absval xml:lang="ja" />
                      <id xml:space="preserve" xml:lang="ja">M</id>
                    </apply>
                  </apply>
                </parens>
                <real xml:lang="ja">1</real>
              </apply>
            </lambda>
            <upperBound xml:lang="ja">
              <placeholder xml:lang="ja" />
            </upperBound>
          </apply>
          <apply xml:lang="ja">
            <summation xml:lang="ja" />
            <lambda xml:lang="ja">
              <boundVars xml:lang="ja">
                <placeholder xml:lang="ja" />
              </boundVars>
              <apply xml:lang="ja">
                <matcol xml:lang="ja" />
                <parens xml:lang="ja">
                  <apply xml:lang="ja">
                    <vectorize xml:lang="ja" />
                    <apply xml:lang="ja">
                      <absval xml:lang="ja" />
                      <id xml:space="preserve" xml:lang="ja">M</id>
                    </apply>
                  </apply>
                </parens>
                <real xml:lang="ja">2</real>
              </apply>
            </lambda>
            <upperBound xml:lang="ja">
              <placeholder xml:lang="ja" />
            </upperBound>
          </apply>
        </matrix>
      </apply>
      <unitOverride xml:lang="ja">
        <placeholder xml:lang="ja" />
      </unitOverride>
    </eval>
  </math>
</region>

クリックしてこの式をコピー

2. norm2関数を使用して M のノルム L2 を求めます。

クリックしてこの式をコピー

3. norme関数を使用して M のユークリッドノルムを求めます。

行列のユークリッドノルムはベクトルのユークリッドノルムに類似しています。

クリックしてこの式をコピー

<region id="ID0EUPZOB" top="1440.0000000000002" left="38.400000000000006" xml:lang="ja" height="60.441333557128914" width="176.66000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="59" xml:lang="ja">
    <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <apply xml:lang="ja">
        <pow xml:lang="ja" />
        <parens xml:lang="ja">
          <apply xml:lang="ja">
            <summation xml:lang="ja" />
            <lambda xml:lang="ja">
              <boundVars xml:lang="ja">
                <id xml:space="preserve" xml:lang="ja">i</id>
              </boundVars>
              <apply xml:lang="ja">
                <summation xml:lang="ja" />
                <lambda xml:lang="ja">
                  <boundVars xml:lang="ja">
                    <id xml:space="preserve" xml:lang="ja">j</id>
                  </boundVars>
                  <apply xml:lang="ja">
                    <pow xml:lang="ja" />
                    <parens xml:lang="ja">
                      <apply xml:lang="ja">
                        <indexer xml:lang="ja" />
                        <id xml:space="preserve" xml:lang="ja">M</id>
                        <sequence xml:lang="ja">
                          <id xml:space="preserve" xml:lang="ja">i</id>
                          <id xml:space="preserve" xml:lang="ja">j</id>
                        </sequence>
                      </apply>
                    </parens>
                    <real xml:lang="ja">2</real>
                  </apply>
                </lambda>
                <lowerBound xml:lang="ja">
                  <real xml:lang="ja">0</real>
                </lowerBound>
                <upperBound xml:lang="ja">
                  <real xml:lang="ja">2</real>
                </upperBound>
              </apply>
            </lambda>
            <lowerBound xml:lang="ja">
              <real xml:lang="ja">0</real>
            </lowerBound>
            <upperBound xml:lang="ja">
              <real xml:lang="ja">2</real>
            </upperBound>
          </apply>
        </parens>
        <apply xml:lang="ja">
          <div xml:lang="ja" />
          <real xml:lang="ja">1</real>
          <real xml:lang="ja">2</real>
        </apply>
      </apply>
      <unitOverride xml:lang="ja">
        <placeholder xml:lang="ja" />
      </unitOverride>
    </eval>
  </math>
</region>

クリックしてこの式をコピー

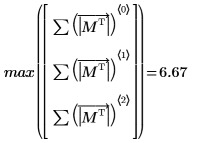
4. M の無限ノルムを求め、結果を関数 normiの出力と比較します。

無限大ノルムは行の絶対値和の最大値です (i=0, 1, 2 の中の最大値)。

クリックしてこの式をコピー

<region id="ID0E1SZOB" top="1651.2000000000003" left="19.200000000000003" xml:lang="ja" height="62.800000000000004" width="134.8366666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="63" xml:lang="ja">
    <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <apply xml:lang="ja">
        <summation xml:lang="ja" />
        <lambda xml:lang="ja">
          <boundVars xml:lang="ja">
            <id xml:space="preserve" xml:lang="ja">j</id>
          </boundVars>
          <apply xml:lang="ja">
            <absval xml:lang="ja" />
            <apply xml:lang="ja">
              <indexer xml:lang="ja" />
              <id xml:space="preserve" xml:lang="ja">M</id>
              <sequence xml:lang="ja">
                <id xml:space="preserve" xml:lang="ja">i</id>
                <id xml:space="preserve" xml:lang="ja">j</id>
              </sequence>
            </apply>
          </apply>
        </lambda>
        <lowerBound xml:lang="ja">
          <real xml:lang="ja">0</real>
        </lowerBound>
        <upperBound xml:lang="ja">
          <real xml:lang="ja">2</real>
        </upperBound>
      </apply>
      <unitOverride xml:lang="ja">
        <placeholder xml:lang="ja" />
      </unitOverride>
    </eval>
  </math>
</region>

クリックしてこの式をコピー

<region id="ID0EMTZOB" top="1766.4000000000003" left="19.200000000000003" xml:lang="ja" height="143.056" width="200.52000000000004" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="65" xml:lang="ja">
    <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <apply xml:lang="ja">
        <id xml:space="preserve" xml:lang="ja">max</id>
        <matrix rows="3" cols="1" xml:lang="ja">
          <apply xml:lang="ja">
            <summation xml:lang="ja" />
            <lambda xml:lang="ja">
              <boundVars xml:lang="ja">
                <placeholder xml:lang="ja" />
              </boundVars>
              <apply xml:lang="ja">
                <matcol xml:lang="ja" />
                <parens xml:lang="ja">
                  <apply xml:lang="ja">
                    <vectorize xml:lang="ja" />
                    <apply xml:lang="ja">
                      <absval xml:lang="ja" />
                      <apply xml:lang="ja">
                        <transpose xml:lang="ja" />
                        <id xml:space="preserve" xml:lang="ja">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real xml:lang="ja">0</real>
              </apply>
            </lambda>
            <upperBound xml:lang="ja">
              <placeholder xml:lang="ja" />
            </upperBound>
          </apply>
          <apply xml:lang="ja">
            <summation xml:lang="ja" />
            <lambda xml:lang="ja">
              <boundVars xml:lang="ja">
                <placeholder xml:lang="ja" />
              </boundVars>
              <apply xml:lang="ja">
                <matcol xml:lang="ja" />
                <parens xml:lang="ja">
                  <apply xml:lang="ja">
                    <vectorize xml:lang="ja" />
                    <apply xml:lang="ja">
                      <absval xml:lang="ja" />
                      <apply xml:lang="ja">
                        <transpose xml:lang="ja" />
                        <id xml:space="preserve" xml:lang="ja">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real xml:lang="ja">1</real>
              </apply>
            </lambda>
            <upperBound xml:lang="ja">
              <placeholder xml:lang="ja" />
            </upperBound>
          </apply>
          <apply xml:lang="ja">
            <summation xml:lang="ja" />
            <lambda xml:lang="ja">
              <boundVars xml:lang="ja">
                <placeholder xml:lang="ja" />
              </boundVars>
              <apply xml:lang="ja">
                <matcol xml:lang="ja" />
                <parens xml:lang="ja">
                  <apply xml:lang="ja">
                    <vectorize xml:lang="ja" />
                    <apply xml:lang="ja">
                      <absval xml:lang="ja" />
                      <apply xml:lang="ja">
                        <transpose xml:lang="ja" />
                        <id xml:space="preserve" xml:lang="ja">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real xml:lang="ja">2</real>
              </apply>
            </lambda>
            <upperBound xml:lang="ja">
              <placeholder xml:lang="ja" />
            </upperBound>
          </apply>
        </matrix>
      </apply>
      <unitOverride xml:lang="ja">
        <placeholder xml:lang="ja" />
      </unitOverride>
    </eval>
  </math>
</region>

クリックしてこの式をコピー

さまざまな行列の条件数

行列の条件数は行列の 2 つのノルムの積です。これは線形連立方程式の解の入力ベクトルの誤差に対する感度の指標です。

クリックしてこの式をコピー

1. cond1関数を使用して M の L1 条件数を求めます。

クリックしてこの式をコピー

2. cond2関数を使用して M の L2 条件数を求めます。

クリックしてこの式をコピー

3. conde関数を使用して M のユークリッド条件数を求めます。

クリックしてこの式をコピー

4. condi関数を使用して M の無限条件数を求めます。

クリックしてこの式をコピー