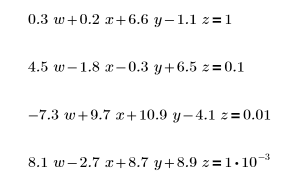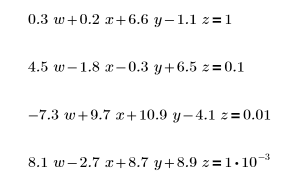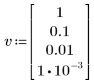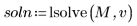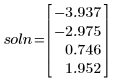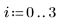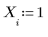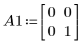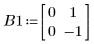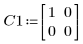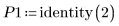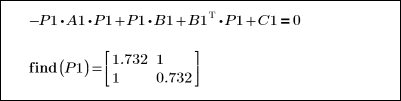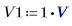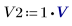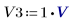例: 連立 1 次方程式の求解
lsolve関数またはソルブブロックを使用して、n 個の未知数を持つ
n 本の方程式から成る線形連立方程式を解きます。
lsolve を使用
1. (「等しい」演算子を使用して定義された) 次の連立方程式があるとします。
2. 上記の連立方程式に対応する正則行列を作成します。
3. 上記の連立方程式に対応する定数ベクトルを作成します。
4. lsolve 関数を使用して解を求めます。
ソルブブロックを使用
上記の連立方程式をソルブブロックを使用して解くこともできます。
| 連立方程式を行列と不明なベクトル X の乗算として変換した場合は、ベクトルのすべての変数を一度に解く必要があります。この公式では、いずれのベクトル成分の定数も保持されません。 |
1. 推定値ベクトル X を指定します。
2. ソルブブロックを挿入し、find 関数を使用して上記の連立方程式を解きます。
| 推定値ベクトル X はソルブブロックの前で定義する必要があります。 |
ソルブブロック - 行列を解く
1. (システム理論や制御理論で使用する) 代数リッカチ方程式を定義します。
2. 初期推定値の行列を単位行列として定義します。
3. find 関数を使用して上記の連立方程式を解きます。
ソルブブロック内の単位
1. V1、V2、V3 を 1 ボルトに設定します。
2. 3 個の未知数を持つ連立方程式を定義して解きます。