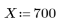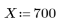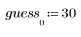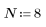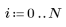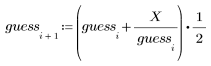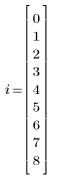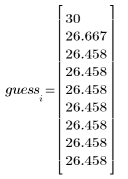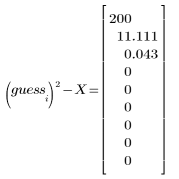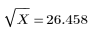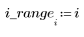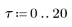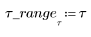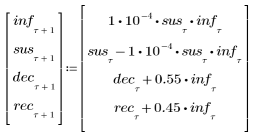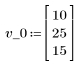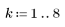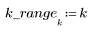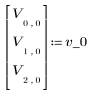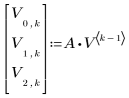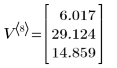例: 種に基づく反復計算と差分方程式
種に基づく反復計算を使用して解を求めます。
平方根
バビロニア法を使用して数値の平方根を近似します。
1. 正の実数 X とその平方根の推定値を定義します。
1 つ目の推定値がベクトルの 1 つ目の成分として定義されます。
2. N を反復回数として定義します。
3. 平方根の新しい推定値を計算します。
平方根の組み込み関数によって次の結果が得られます。
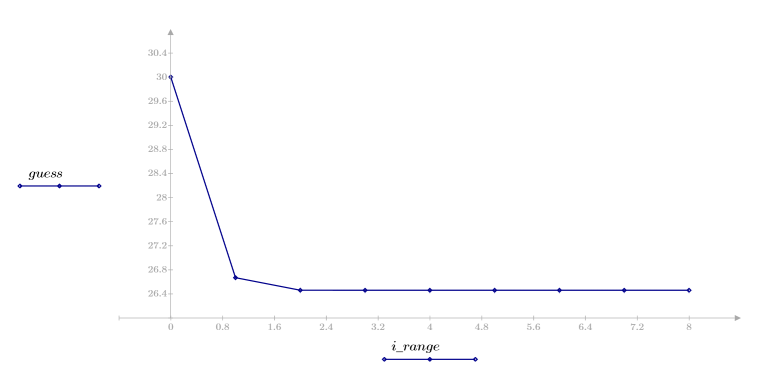
4. 推定値のベクトルをプロットします。
ここでは、急激に収束しています。その他の場合、問題に応じて反復回数 N の値を増やすことができます。
連立差分方程式
4 つの変数を使って感染モデルを考えます。
• inf - 感染者の人数
• sus - 感染の可能性がある人の数
• dec - 死亡した人の数
• rec - 回復した人の数
1. 同時反復計算のためのシード値を定義します。
2. 連立差分方程式を定義します。
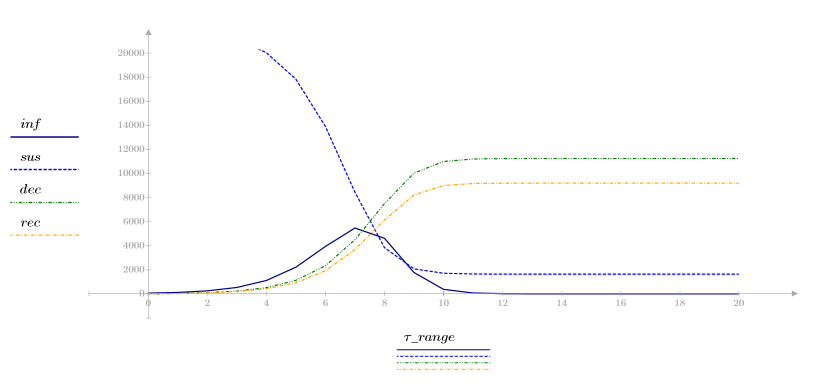
3. 4 つの変数を時間に対してプロットして感染モデルの推移を調べます。
行列差分方程式
マルコフ過程を考えます。これは、元の状態と状態遷移行列の乗算により現在の状態が求められるベクトル時系列です。
1. 初期状態ベクトルと状態遷移行列 A を定義します。
2. 反復プロセスを定義します。
3. 最終状態ベクトルを計算します。
行列 V に全過程が格納されます。