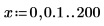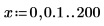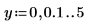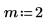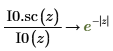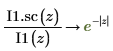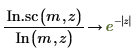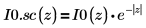例: 第 1 種変形ベッセル関数
関数
I0、
I1、および
Inの関係を示します。関数とその尺度化された型との関係も表示します。
1. 2 つのレンジ変数を次のように定義します。
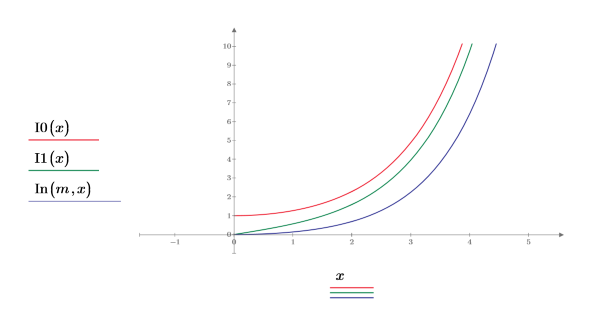
2. 関数 I0 と I1 をプロットします。2 次関数 In をプロットに次のように追加します。
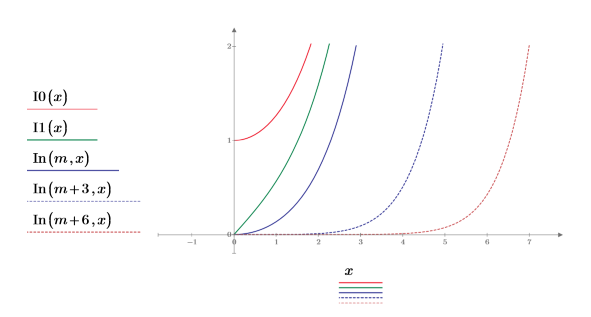
3. 5 次および 8 次関数 In を次のようにプロットします。
| • In 関数の次数が高いほど、0 から無限大への遷移は急峻になります。 • 関数 I0 のみが (x=0,y=1) を原点とします。その他のすべての次数の原点は (x=0,y=0). になります。 |
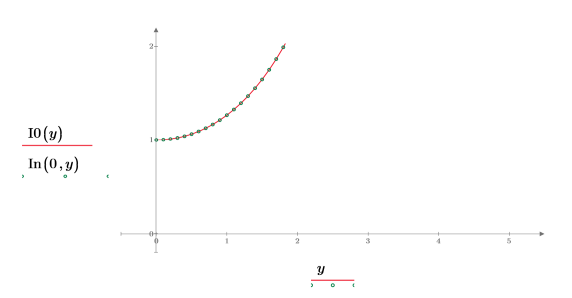
4. 次を示すプロットを作成します。I0(y)=In(0,y)目盛の値をリセットして、X 軸を拡大してより詳細に表示します。
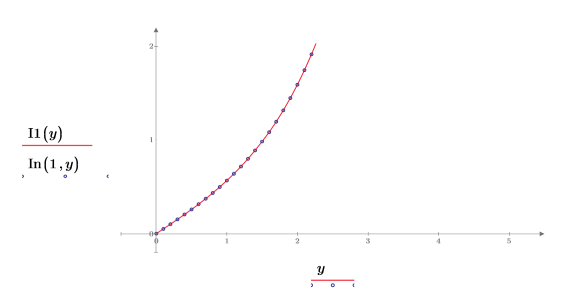
5. 次を示すプロットを作成します。I1(y)=In(1,y)目盛の値をリセットして、X 軸を拡大してより詳細に表示します。
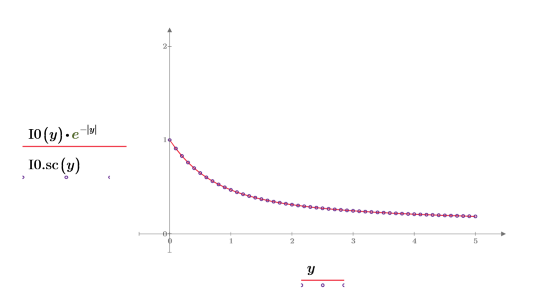
6. シンボリック評価を使用して、各関数とその尺度化された型の関係を次のように表示します。
7. プロットして次のことを示します。
第 1 種変形ベッセル関数にはピークはありません。