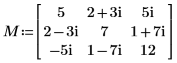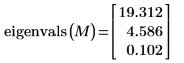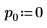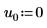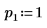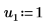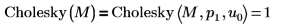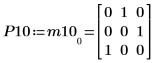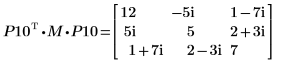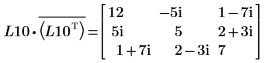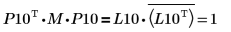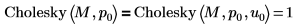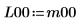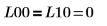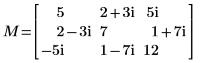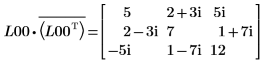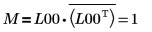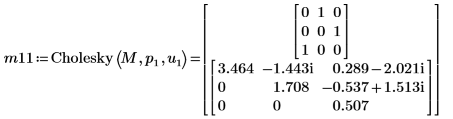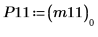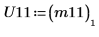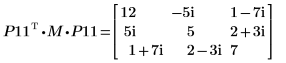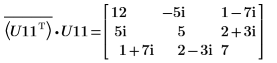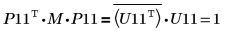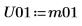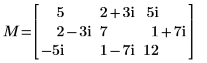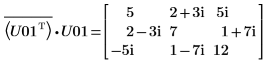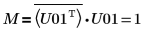例: 複素行列のコレスキー分解
Cholesky関数を使用して、複素行列
Hermitian の
Cholesky 分解を実行します。
|
|
ブール比較実行時の論理不一致を避けるには、「計算オプション」ドロップダウンリストの「近似等価」を有効にします。
|
1. Hermitian 定値複素正方行列 M を定義します。
3. 引数 p と u を設定して、ピボットおよび上/下三角行列への分解の有効/無効を制御します。
4. Cholesky 関数を使用して行列 M のデフォルトの分解 (ピボットあり、下三角行列への分解) を実行します。
| デフォルト関数 Cholesky(M) は Cholesky(M,1,0) と等価です。 |
5. P10T x M x P10 = L10 x conj(L10T) を表示します。
関係は論理的に真です。
6. Cholesky 関数を使用して行列 M の分解 (ピボットなし、下三角行列への分解 (デフォルト)) を実行します。
| 引数 u を指定しない場合 (Cholesky(M, 0) 内など) は、Cholesky(M, 0, 0) で 0 を設定した場合に等しくなります。 |
| ピボットを有効にしたときに返される下三角行列 L10 は、ピボットを無効にしたときに返される下三角行列 L00 とは等しくなりません。 関係は論理的に偽です。 |
7. M = L00 x conj(L00T) を表示します。
関係は論理的に真です。
8. Cholesky 関数を使用して行列 M の分解 (ピボットあり、上三角行列への分解) を実行します。
9. P11T x M x P11 = conj(U11T) x U11 を表示します。
関係は論理的に真です。
10. Cholesky 関数を使用して行列 M の分解 (ピボットなし、上三角行列への分解) を実行します。
11. M = conj(U01T) x U01 を表示します。
関係は論理的に真です。