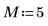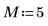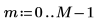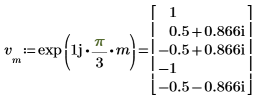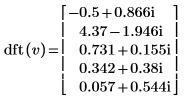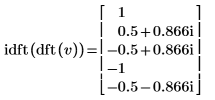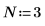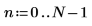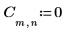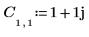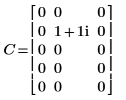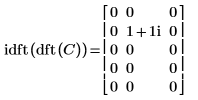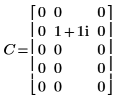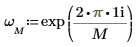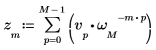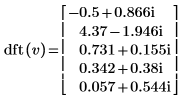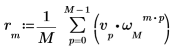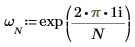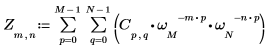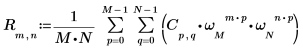例: 逆変換 idft
idft関数は
dftの逆変換なので、複素変換への入力データが復元されることが予想されます。
ベクトル (1 D) の使用
1. ベクトル v の長さを定義します。
2.
exp関数を使用して、ベクトル
v を定義および評価します。
3. dft 関数を使用して、ベクトル v の順変換を計算します。
4. idft 関数を使用して、ベクトル v の逆変換を計算します。
5. ベクトル v の順変換を逆変換したものは、元のベクトル v になることを示します。
結果は等しくなります。
行列 (2 D) の使用
1. 行列 C を定義して評価します。
2. dft 関数を使用して、行列 C の順変換を計算します。
3. idft 関数を使用して、行列 C の逆変換を計算します。
4. 行列 C の順変換を逆変換したものは、元の行列 C になることを示します。
結果は等しくなります。
idft の基礎となる和の説明
1 次元の場合:
1. exp 関数と sum 演算子を使用して、ベクトル v の逆変換を計算します。
2. 結果となるベクトル v の順変換を dft 関数の出力と比較します。
結果は等しくなります。
3. sum 演算子を使用して、ベクトル v の逆変換を計算します。
4. 結果となるベクトル v の逆変換を idft 関数の出力と比較します。
結果は等しくなります。
2 次元の場合:
1. exp 関数と sum 演算子を使用して、行列 C の順変換を計算します。
2. 結果となる行列 C の順変換を dft 関数の出力と比較します。
結果は等しくなります。
3. sum 演算子を使用して、行列 C の逆変換を計算します。
4. 結果となる行列 C の逆変換を idft 関数の出力と比較します。
結果は等しくなります。