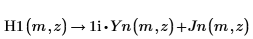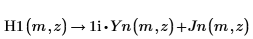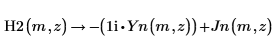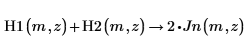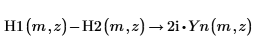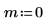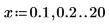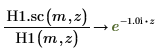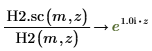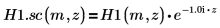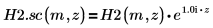例: 1 次および 2 次のハンケル関数
ハンケル関数
H1および
H2とベッセル関数
Jnおよび
Ynの関係を示します。関数とその尺度化された型との関係も表示します。
ハンケル関数は 0 においては定義されていません。
1. シンボリック評価を使用して、H1、Jn、および Yn の関係を次のように示します。
2. シンボリック評価を使用して、H2、Jn、および Yn の関係を次のように示します。
◦ H1 と H2 の実数成分は、値も符号も同一です。
◦ H1 と H2 の虚数成分は、値は同じですが符号が逆です。
3. H1 と H2 の間には、これらの 2 つの別の重要な関係があることに注意してください。
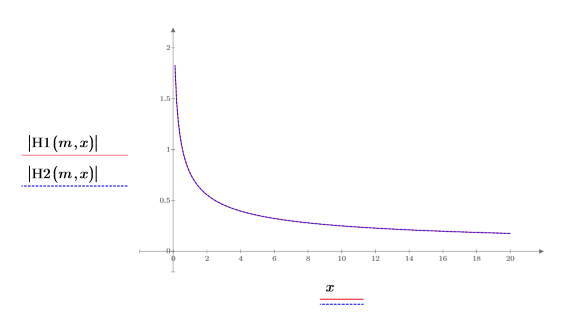
4. プロットを作成して、|H1|=|H2| であることを視覚的に示します。
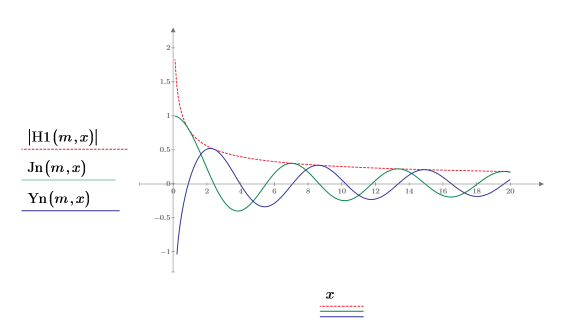
5. プロットを作成して、H1、Jn、および Yn の関係を次のように示します。
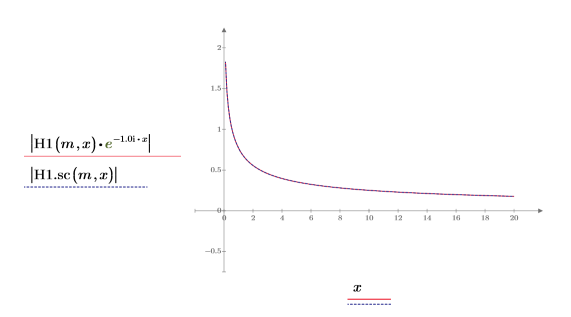
6. シンボリック評価を使用して、ハンケル関数とその尺度化された型の関係を次のように表示します。
7. 次を示すプロットを作成します。
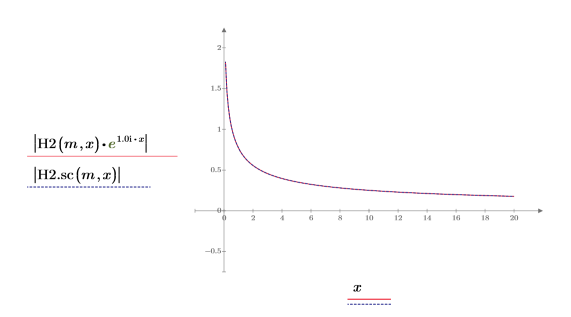
8. 次を示すプロットを作成します。