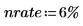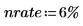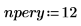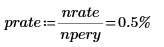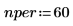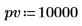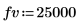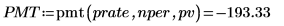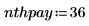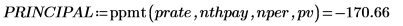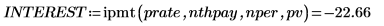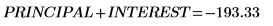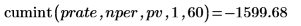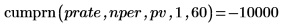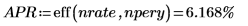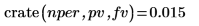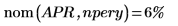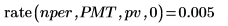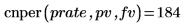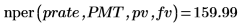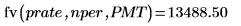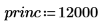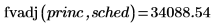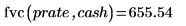1. 年利率を定義します。

2. 1 年あたりの複利計算期間の数を定義します。

3. 定期利率を定義します。

4. 複利計算期間の数を定義します。

5. ローンの現在価値と将来価値を定義します。

1. pmt関数を使用して、10,000 ドルのローンを年利 6% で 5 年間で返済する場合に必要な月々の支払額を計算します。

2. ppmt関数を使用して、36 カ月目のローンの元金支払額を計算します。

3. ipmt関数を使用して、36 カ月目のローンの利息支払額を計算します。

1. cumint関数を使用して、前述のローンで支払われる累積利息を計算します。

2. cumprn関数を使用して、前述のローンで支払われる累積元金を計算します。

3. eff関数を使用して、前述のローンで支払われる実質年利 (APR) を計算します。

1. crate関数を使用して、投資を指定した将来価値 fv にするために必要な固定利率を計算します。現在価値 pv と複利計算期間数 nper を引数として指定します。

2. nom関数を使用して、前述の APR に対応する名目利率を計算します。

3. rate関数を使用して、複利計算期間の数が nper の場合の、期間ごとの利率を計算します。一定の固定期間支払 pmt と現在価値 pv を引数として指定します。

1. 関数 cnperを使用して、年利が prate であると仮定した場合に投資 pv が fv に達するまでの複利計算期間の数を求めます。

2. 関数 nperを使用して、月々の支払いが PMT、年利が prate であると仮定した場合に投資 pv が fv に達するまでの期間数を求めます。

1. fv関数を使用して、定期的な一定額 PMT が複利計算期間の数 nper にわたって固定利率 prate で支払われる場合の投資の将来価値を計算します。

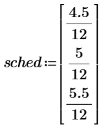
2. fvadj関数を使用して、一連の複利利率 sched を適用した場合の初期元金 princ の将来価値を計算します。

3. fvc関数を使用して、利率 prate を得る通常の期間に発生する一連のキャッシュフローの将来価値を計算します。