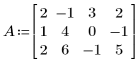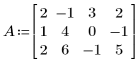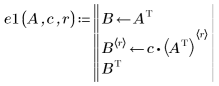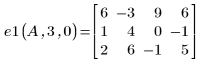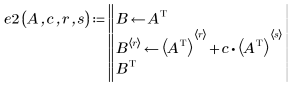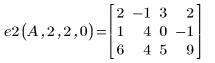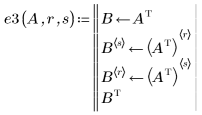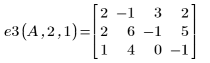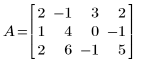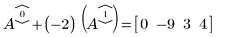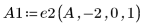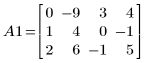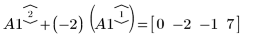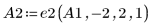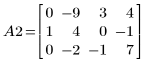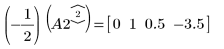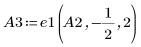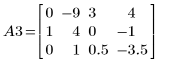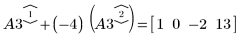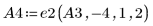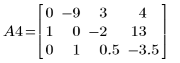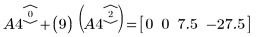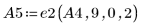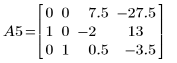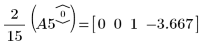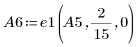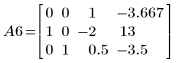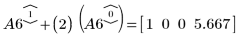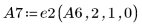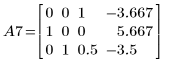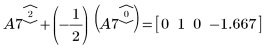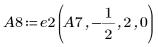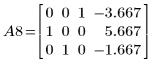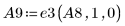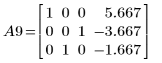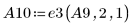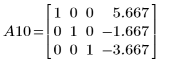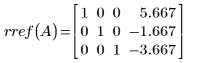例: 行列の行基本変形

ベクトル、行列、テーブル > 配列およびテーブルの作成 > 例: 行列の行基本変形

例: 行列の行基本変形

m x n の行列に対して 3 種類の行基本変形を行い、被約階段行列との関連性を示します。

1. 入力行列を定義します。

クリックしてこの式をコピー

2. 行 r にスカラー c を掛け合わせます。

クリックしてこの式をコピー

<region id="ID0EBSMOB" top="144" left="24" xml:lang="ja" height="85.656" width="217.526666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math xml:lang="ja">
    <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <function xml:lang="ja">
        <id xml:lang="ja" label="Variable">e1</id>
        <boundVars xml:lang="ja">
          <id xml:lang="ja" label="Variable">A</id>
          <id xml:lang="ja" label="Variable">c</id>
          <id xml:lang="ja" label="Variable">r</id>
        </boundVars>
      </function>
      <program xml:lang="ja">
        <localDefine xml:lang="ja">
          <id xml:lang="ja" label="Variable">B</id>
          <apply xml:lang="ja">
            <transpose xml:lang="ja" />
            <id xml:lang="ja">A</id>
          </apply>
        </localDefine>
        <localDefine xml:lang="ja">
          <apply xml:lang="ja">
            <matcol xml:lang="ja" />
            <id xml:lang="ja" label="Variable">B</id>
            <id xml:lang="ja" label="Variable">r</id>
          </apply>
          <apply xml:lang="ja">
            <mult xml:lang="ja" />
            <id xml:lang="ja">c</id>
            <apply xml:lang="ja">
              <matcol xml:lang="ja" />
              <parens xml:lang="ja">
                <apply xml:lang="ja">
                  <transpose xml:lang="ja" />
                  <id xml:lang="ja">A</id>
                </apply>
              </parens>
              <id xml:lang="ja">r</id>
            </apply>
          </apply>
        </localDefine>
        <apply xml:lang="ja">
          <transpose xml:lang="ja" />
          <id xml:lang="ja">B</id>
        </apply>
      </program>
    </define>
  </math>
</region>

クリックしてこの式をコピー

3. 行 r を、行 r に行 s の c 倍を加えたものに置き換えます。

クリックしてこの式をコピー

<region id="ID0E3UMOB" top="360" left="24" xml:lang="ja" height="85.656" width="291.823333333333" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math xml:lang="ja">
    <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <function xml:lang="ja">
        <id xml:lang="ja" label="Variable">e2</id>
        <boundVars xml:lang="ja">
          <id xml:lang="ja" label="Variable">A</id>
          <id xml:lang="ja" label="Variable">c</id>
          <id xml:lang="ja" label="Variable">r</id>
          <id xml:lang="ja" label="Variable">s</id>
        </boundVars>
      </function>
      <program xml:lang="ja">
        <localDefine xml:lang="ja">
          <id xml:lang="ja" label="Variable">B</id>
          <apply xml:lang="ja">
            <transpose xml:lang="ja" />
            <id xml:lang="ja">A</id>
          </apply>
        </localDefine>
        <localDefine xml:lang="ja">
          <apply xml:lang="ja">
            <matcol xml:lang="ja" />
            <id xml:lang="ja" label="Variable">B</id>
            <id xml:lang="ja" label="Variable">r</id>
          </apply>
          <apply xml:lang="ja">
            <plus xml:lang="ja" />
            <apply xml:lang="ja">
              <matcol xml:lang="ja" />
              <parens xml:lang="ja">
                <apply xml:lang="ja">
                  <transpose xml:lang="ja" />
                  <id xml:lang="ja">A</id>
                </apply>
              </parens>
              <id xml:lang="ja">r</id>
            </apply>
            <apply xml:lang="ja">
              <mult xml:lang="ja" />
              <id xml:lang="ja">c</id>
              <apply xml:lang="ja">
                <matcol xml:lang="ja" />
                <parens xml:lang="ja">
                  <apply xml:lang="ja">
                    <transpose xml:lang="ja" />
                    <id xml:lang="ja">A</id>
                  </apply>
                </parens>
                <id xml:lang="ja">s</id>
              </apply>
            </apply>
          </apply>
        </localDefine>
        <apply xml:lang="ja">
          <transpose xml:lang="ja" />
          <id xml:lang="ja">B</id>
        </apply>
      </program>
    </define>
  </math>
</region>

クリックしてこの式をコピー

4. 行 r と行 s を入れ替えます。

クリックしてこの式をコピー

<region id="ID0ENXMOB" top="552" left="24" xml:lang="ja" height="114.808" width="200.72" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math xml:lang="ja">
    <define xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <function xml:lang="ja">
        <id xml:lang="ja" label="Variable">e3</id>
        <boundVars xml:lang="ja">
          <id xml:lang="ja" label="Variable">A</id>
          <id xml:lang="ja" label="Variable">r</id>
          <id xml:lang="ja" label="Variable">s</id>
        </boundVars>
      </function>
      <program xml:lang="ja">
        <localDefine xml:lang="ja">
          <id xml:lang="ja" label="Variable">B</id>
          <apply xml:lang="ja">
            <transpose xml:lang="ja" />
            <id xml:lang="ja">A</id>
          </apply>
        </localDefine>
        <localDefine xml:lang="ja">
          <apply xml:lang="ja">
            <matcol xml:lang="ja" />
            <id xml:lang="ja" label="Variable">B</id>
            <id xml:lang="ja" label="Variable">s</id>
          </apply>
          <apply xml:lang="ja">
            <matcol xml:lang="ja" />
            <parens xml:lang="ja">
              <apply xml:lang="ja">
                <transpose xml:lang="ja" />
                <id xml:lang="ja">A</id>
              </apply>
            </parens>
            <id xml:lang="ja">r</id>
          </apply>
        </localDefine>
        <localDefine xml:lang="ja">
          <apply xml:lang="ja">
            <matcol xml:lang="ja" />
            <id xml:lang="ja" label="Variable">B</id>
            <id xml:lang="ja" label="Variable">r</id>
          </apply>
          <apply xml:lang="ja">
            <matcol xml:lang="ja" />
            <parens xml:lang="ja">
              <apply xml:lang="ja">
                <transpose xml:lang="ja" />
                <id xml:lang="ja">A</id>
              </apply>
            </parens>
            <id xml:lang="ja">s</id>
          </apply>
        </localDefine>
        <apply xml:lang="ja">
          <transpose xml:lang="ja" />
          <id xml:lang="ja">B</id>
        </apply>
      </program>
    </define>
  </math>
</region>

クリックしてこの式をコピー

行列の被約階段行列

被約階段行列は線形連立方程式を解く場合に使用される重要な手法です。

行列 A の被約階段行列を求めるには、次に示す e1、e2、e3 による一連の操作を行います。

1. 行列 A を定義します。

クリックしてこの式をコピー

2. e2 を使用して、A の行 0 を、行 0 に行 1 の (-2) 倍を加えたものに置き換えます。

クリックしてこの式をコピー

<region id="ID0EZ4MOB" top="912" left="24" xml:lang="ja" height="36.552" width="225.99" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="50" xml:lang="ja">
    <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <apply xml:lang="ja">
        <plus xml:lang="ja" />
        <apply xml:lang="ja">
          <matrow xml:lang="ja" />
          <id xml:lang="ja">A</id>
          <real xml:lang="ja">0</real>
        </apply>
        <apply xml:lang="ja">
          <scale xml:lang="ja" />
          <parens xml:lang="ja">
            <real xml:lang="ja">-2</real>
          </parens>
          <parens xml:lang="ja">
            <apply xml:lang="ja">
              <matrow xml:lang="ja" />
              <id xml:lang="ja">A</id>
              <real xml:lang="ja">1</real>
            </apply>
          </parens>
        </apply>
      </apply>
      <unitOverride xml:lang="ja">
        <placeholder xml:lang="ja" />
      </unitOverride>
    </eval>
  </math>
</region>

クリックしてこの式をコピー

クリックしてこの式をコピー

3. e2 を使用して、A1 の行 2 を、行 2 に行 1 の (-2) 倍を加えたものに置き換えます。

クリックしてこの式をコピー

<region id="ID0EPBNOB" top="1032" left="24" xml:lang="ja" height="36.552" width="252.7" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="52" xml:lang="ja">
    <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <apply xml:lang="ja">
        <plus xml:lang="ja" />
        <apply xml:lang="ja">
          <matrow xml:lang="ja" />
          <id xml:lang="ja">A1</id>
          <real xml:lang="ja">2</real>
        </apply>
        <apply xml:lang="ja">
          <scale xml:lang="ja" />
          <parens xml:lang="ja">
            <real xml:lang="ja">-2</real>
          </parens>
          <parens xml:lang="ja">
            <apply xml:lang="ja">
              <matrow xml:lang="ja" />
              <id xml:lang="ja">A1</id>
              <real xml:lang="ja">1</real>
            </apply>
          </parens>
        </apply>
      </apply>
      <unitOverride xml:lang="ja">
        <placeholder xml:lang="ja" />
      </unitOverride>
    </eval>
  </math>
</region>

クリックしてこの式をコピー

クリックしてこの式をコピー

4. e1 を使用して、A2 の行 2 を (-1/2) 倍します。

クリックしてこの式をコピー

クリックしてこの式をコピー

クリックしてこの式をコピー

5. e2 を使用して、A3 の行 1 を、行 1 に行 2 の (-4) 倍を加えたものに置き換えます。

クリックしてこの式をコピー

<region id="ID0ERINOB" top="1344" left="24" xml:lang="ja" height="36.552" width="249.93" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="56" xml:lang="ja">
    <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <apply xml:lang="ja">
        <plus xml:lang="ja" />
        <apply xml:lang="ja">
          <matrow xml:lang="ja" />
          <id xml:lang="ja">A3</id>
          <real xml:lang="ja">1</real>
        </apply>
        <apply xml:lang="ja">
          <scale xml:lang="ja" />
          <parens xml:lang="ja">
            <real xml:lang="ja">-4</real>
          </parens>
          <parens xml:lang="ja">
            <apply xml:lang="ja">
              <matrow xml:lang="ja" />
              <id xml:lang="ja">A3</id>
              <real xml:lang="ja">2</real>
            </apply>
          </parens>
        </apply>
      </apply>
      <unitOverride xml:lang="ja">
        <placeholder xml:lang="ja" />
      </unitOverride>
    </eval>
  </math>
</region>

クリックしてこの式をコピー

クリックしてこの式をコピー

6. e2 を使用して、A4 の行 0 を、行 0 に行 2 の (9) 倍を加えたものに置き換えます。

クリックしてこの式をコピー

<region id="ID0EHMNOB" top="1536" left="24" xml:lang="ja" height="36.552" width="263.88" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="58" xml:lang="ja">
    <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <apply xml:lang="ja">
        <plus xml:lang="ja" />
        <apply xml:lang="ja">
          <matrow xml:lang="ja" />
          <id xml:lang="ja">A4</id>
          <real xml:lang="ja">0</real>
        </apply>
        <apply xml:lang="ja">
          <scale xml:lang="ja" />
          <parens xml:lang="ja">
            <real xml:lang="ja">9</real>
          </parens>
          <parens xml:lang="ja">
            <apply xml:lang="ja">
              <matrow xml:lang="ja" />
              <id xml:lang="ja">A4</id>
              <real xml:lang="ja">2</real>
            </apply>
          </parens>
        </apply>
      </apply>
      <unitOverride xml:lang="ja">
        <placeholder xml:lang="ja" />
      </unitOverride>
    </eval>
  </math>
</region>

クリックしてこの式をコピー

クリックしてこの式をコピー

7. e1 を使用して、A5 の行 0 を 2/15 倍します。

クリックしてこの式をコピー

クリックしてこの式をコピー

クリックしてこの式をコピー

8. e2 を使用して、A6 の行 1 を、行 1 に行 0 の (2) 倍を加えたものに置き換えます。

クリックしてこの式をコピー

<region id="ID0EJTNOB" top="1920" left="24" xml:lang="ja" height="36.552" width="248.76" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="62" xml:lang="ja">
    <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <apply xml:lang="ja">
        <plus xml:lang="ja" />
        <apply xml:lang="ja">
          <matrow xml:lang="ja" />
          <id xml:lang="ja">A6</id>
          <real xml:lang="ja">1</real>
        </apply>
        <apply xml:lang="ja">
          <scale xml:lang="ja" />
          <parens xml:lang="ja">
            <real xml:lang="ja">2</real>
          </parens>
          <parens xml:lang="ja">
            <apply xml:lang="ja">
              <matrow xml:lang="ja" />
              <id xml:lang="ja">A6</id>
              <real xml:lang="ja">0</real>
            </apply>
          </parens>
        </apply>
      </apply>
      <unitOverride xml:lang="ja">
        <placeholder xml:lang="ja" />
      </unitOverride>
    </eval>
  </math>
</region>

クリックしてこの式をコピー

クリックしてこの式をコピー

9. e2 を使用して、A7 の行 2 を、行 2 に行 0 の (-1/2) 倍を加えたものに置き換えます。

クリックしてこの式をコピー

<region id="ID0E6WNOB" top="2064" left="24" xml:lang="ja" height="48.5106666666667" width="275.133333333333" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="64" xml:lang="ja">
    <eval xml:lang="ja" xmlns="http://schemas.mathsoft.com/math50">
      <apply xml:lang="ja">
        <plus xml:lang="ja" />
        <apply xml:lang="ja">
          <matrow xml:lang="ja" />
          <id xml:lang="ja">A7</id>
          <real xml:lang="ja">2</real>
        </apply>
        <apply xml:lang="ja">
          <scale xml:lang="ja" />
          <parens xml:lang="ja">
            <apply xml:lang="ja">
              <neg xml:lang="ja" />
              <apply xml:lang="ja">
                <div xml:lang="ja" />
                <real xml:lang="ja">1</real>
                <real xml:lang="ja">2</real>
              </apply>
            </apply>
          </parens>
          <parens xml:lang="ja">
            <apply xml:lang="ja">
              <matrow xml:lang="ja" />
              <id xml:lang="ja">A7</id>
              <real xml:lang="ja">0</real>
            </apply>
          </parens>
        </apply>
      </apply>
      <unitOverride xml:lang="ja">
        <placeholder xml:lang="ja" />
      </unitOverride>
    </eval>
  </math>
</region>

クリックしてこの式をコピー

クリックしてこの式をコピー

10. e3 を使用して、A8 の行 0 と行 1 を入れ替えます。

クリックしてこの式をコピー

クリックしてこの式をコピー

11. e3 を使用して、A9 の行 1 と行 2 を入れ替えます。

クリックしてこの式をコピー

クリックしてこの式をコピー

この例では、上記の一連の行基本変形によって、行列 A の被約階段行列が求められます。

12. rref関数を使用して、行列 A の被約階段行列を求めます。

クリックしてこの式をコピー

返される行列は行列 A10 と同じです。