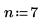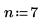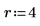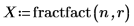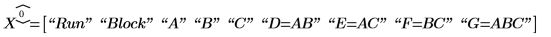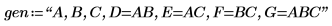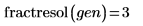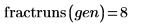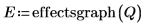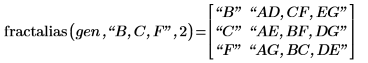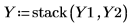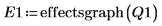例: 因子のエイリアス解除
A:
視力
B:
対象物から目までの距離
C:
対象物の形状
D:
照明レベル
E:
対象物のサイズ
F:
密度
G:
被験者
重要な因子の数は少なく、因子間の高次交互作用は無視できるものとします。
1.
2.
3. fractfact を呼び出して、計画行列 X を作成します。
4. gen を定義して、計画行列 X の因子とエイリアスを格納します。
5. fractresol と fractruns を呼び出して、計画行列 X の分解能とラン数を求めます。
計画行列 X は分解能 III、ラン数 8 の部分因子計画行列を表しています (その主因子は別の主因子のエイリアスではなく、2 次交互作用のエイリアスです)。
6. Y1 に格納します。行列の行によってどのランのデータであるかを識別し、列によってどのレプリケートのデータであるかを識別します。
7. quickscreen 関数を呼び出します。
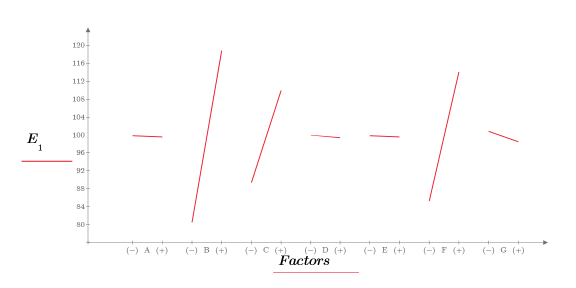
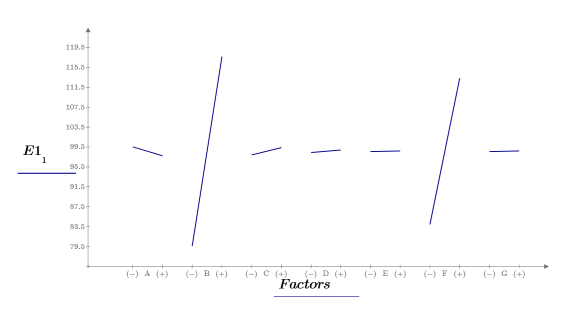
8. effectsgraph 関数を呼び出して効果グラフを作成し、有意因子を特定します。
因子 B 、C 、F には大きな効果が見られます。
9. fractalias を呼び出して、どの 2 次交互作用が B 、C 、F のエイリアスであるかを調べます。
B と C が有意因子である場合、交互作用 BC も有意である可能性が高くなります。BC は F のエイリアスなので、F の効果は F と BC のどちらによるものなのかわかりません。同様の問題は B と F や C と F についても起こります。主因子と 2 次交互作用との間のエイリアスを解除する必要があります。
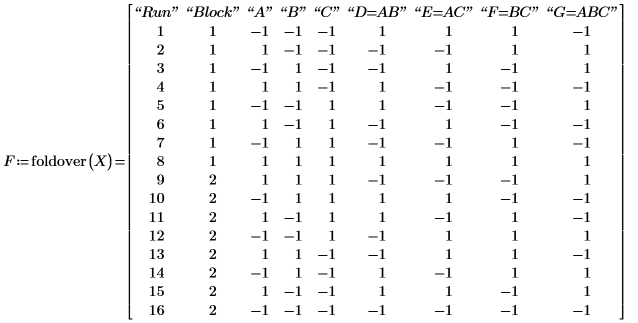
10. foldover を呼び出して計画行列 X を折り返し (符号を反転させて複製し)、主因子と 2 次交互作用との間のエイリアスを解除します。
行列 X の 8 つの行が符号が反転されて F の下半分に格納されます。特定の因子を選択して foldover を実行できます。
11. F の下半分) を実行し、その結果を格納します。
12. Y で元のランと追加のランを積み重ねます。
13. quickscreen と effectsgraph を呼び出して効果グラフを作成し、因子効果を特定します。
因子 B と F だけが有意因子です。したがって、因子 C で先に見られた効果は交互作用 BF によるものでした。さらに実験を行って、因子 B (対象物から目までの距離) と因子 F (密度) が焦点時間に与える影響を分析できます。
参考文献
Montgomery, D.C., Design and Analysis of Experiments , 5th ed, John Wiley & Sons, New York, 2001, pp.341.
式をコピー