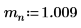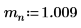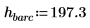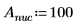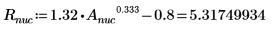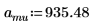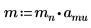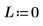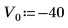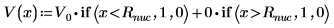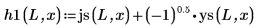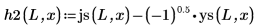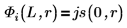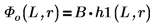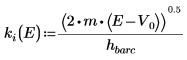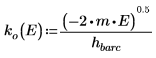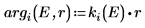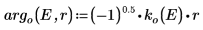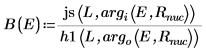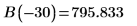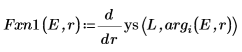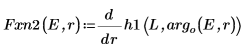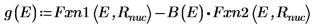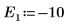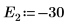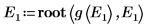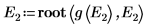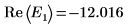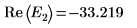例: ベッセル関数
球ベッセル関数と球ハンケル関数を使用して、正立方体の井戸 (原子) におけるシュレディンガー方程式の解を求めます。
この解は、内外の波動関数の値と 1 つ目の導関数が等しくなるときの許容エネルギーを表します。このようなエネルギーは角運動量 (l) の各値に存在します。
1. 質量、プランク定数、原子核半径を定義します。
2. 角運動量をゼロに設定します。
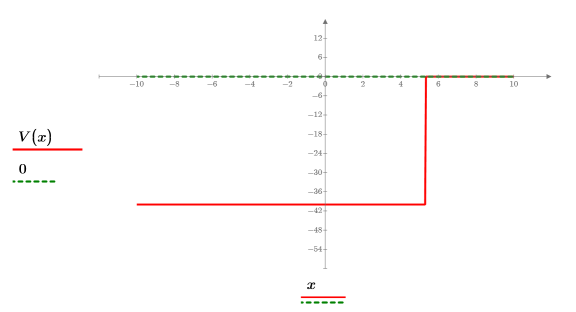
3. 井戸型ポテンシャルのエネルギーを定義してプロットします。
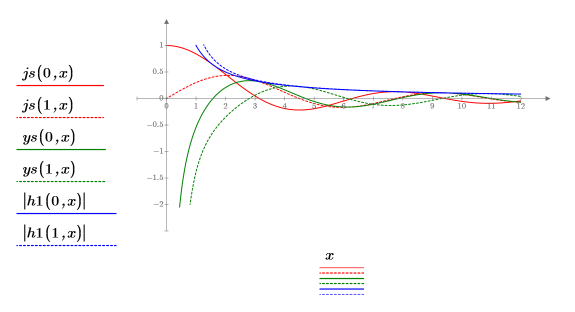
4. 球ベッセル関数と球ハンケル関数を使用して解を求めます。
5. 束縛状態 E < 0 の場合について、井戸の内側と外側における 1 つ目のエネルギー状態の解の波動関数を定義します。
B は相対正規化項です。
6. 伝搬定数を定義します。
波は井戸型ポテンシャルの外側で崩壊するので、井戸の外側の解の引数は虚数です。
7. 井戸のエッジ (原子核の半径) における 2 つの波動関数を一致させることで相対正規化項を求めます。
8. 導関数を一致させます。導関数が等しくなる場所を見つけることで固有値を求めます。
9. E の 2 つの推定値を次のように指定します。
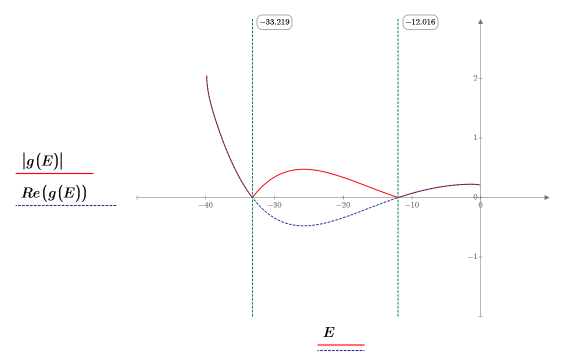
10. g(E) 対 E をプロットして、次のように縦マーカーを追加して 2 つのルート点を表示します。