多變量多項式遞歸

• polyfit(X, Y, n/"terms"/M) - 定義說明多變量多項式遞歸曲面將矩陣 Y 中記錄的結果擬合矩陣 X 中所求得之數據的函數。您可依多項式遞歸方程式的多項式冪次 n 或依其在字串 “terms” 或矩陣 M 中指定的項數，定義多項式遞歸方程式。若不想在擬合多項式中包括截距，請使用矩陣 M。

以多項式遞歸函數 p 為例：

p := polyfit(X, Y ,1)

p(v) = 1.075

函數 p 採用指定 p 的每個自變數值的向量引數 v，如矩陣 X 所述。向量 v 中的每個變數都必須具有與矩陣 X 之對應欄相容的單位。擬合函數 p 傳回的單位與矩陣 Y 的單位相容。

引數

• X 是設計矩陣或矩陣，其中每一欄各代表一個自變數。X 的每一欄都必須具有相容的單位。

• Y 是量測或模擬結果的向量或矩陣，其中每一列包含 X 中所定義之每次執行或每個數據點的結果。若每一列所含的複製數目不一定相同，則必須以 NaN 填補 Y 的空白元素。矩陣 Y 的元素必須具有相容的單位。

• n 是指定多項式階數的整數。它必須小於數據點的總數：1 ≤ n ≤ length(Y) − 1。否則，問題會受限為沒有唯一的解。

• “terms” 是指定要包括在多項式遞歸中之項數 (或係數與相互作用) 的字串。"A B AB AA BB" 表示多項式包含下列項數：

c0 + c1 ∙ A + c2 ∙ B + c3 ∙ A ∙ B + c4 ∙ A2 + c5 ∙ B2

您可以使用空格、逗號、冒號或分號作為分隔符號。

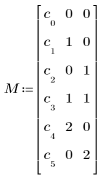
• M 是指定多項式的矩陣，其第一欄中含有係數的估值，而剩餘欄中則含有每個項數的自變數次方。針對上述多項式，如下定義 M：