範例:雜訊產生器
白雜訊
whiten 函數模擬 N 個獨立來源所產生的雜訊,它們每一個在介於 -0.5 及 0.5 間的均等分佈之後,都會跟著隨機輸出。
1. 使用 whiten 函數計算六個獨立雜訊來源的白雜訊函數。

重複計算 whiten 函數,會得出不同的向量元素集合。
2. 考慮稍微大一些的輸出向量。
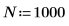
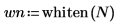
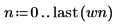
3. 繪製白雜訊函數。
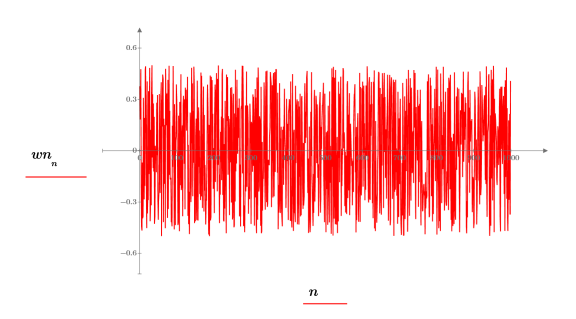
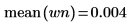
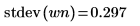
5. 顯示均數的理論值,然後使用 var 函數計算標準差。
繪圖會顯示 wn 信號的理論均數為 0。 | |
標準差是變異數的平方根。 | 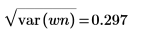 |
6. 比較計算出的均數及標準差值與其理論值,並確認它們彼此不會明顯偏離。
高斯雜訊
gaussn 函數模擬 x 個獨立雜訊來源,每個皆跟在均數為 0 且標準差為 1 的高斯機率分佈之後。
1. 計算六個獨立雜訊來源的 gaussian 雜訊函數。

向量中的元素理論上可為任何實數,但最可能落在 -3 及 +3 之間。您可以透過按 F5 重新計算函數來進行核對。
2. 繪製樣本高斯序列。
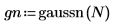
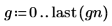
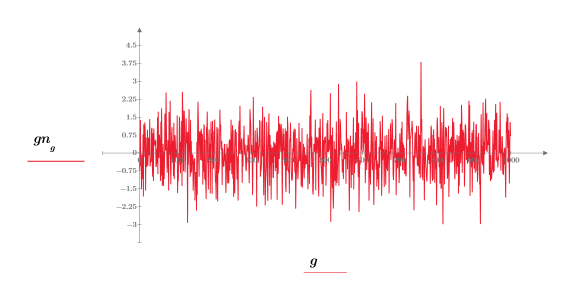
3. 將值分組到寬度為 0.05 的 20 個長條中,以準備鐘形長條圖的高斯數據。
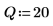
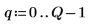
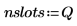
4. 定義向量,該向量保留柱狀的邊緣,然後設定最右側邊界。
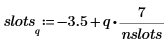
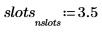
5. 使用 hist 函數建立長條圖,然後將其繪製為柱狀圖。
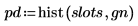
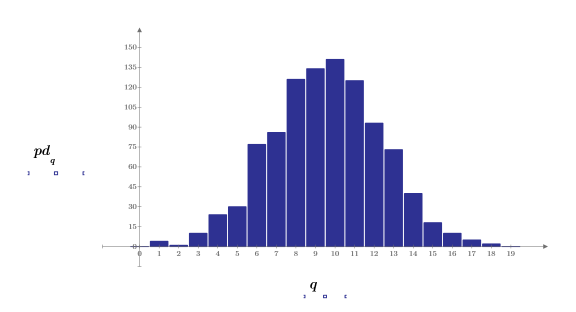
6. 比較樣本的均數及標準差與預期的值 0 及 1。
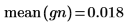
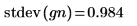
1/f 雜訊
onefn 函數使用以 Richard Voss 開發之演算法為基礎的常式 (請參閱 1978 年 4 月號《科學人》雜誌 Martin Gardner 的專欄),計算 1/f 雜訊的近似值。
1. 使用 onefn 函數產生 1000 個點的 1/f 向量。
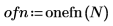
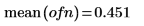
2. 調整至均數 0。
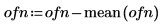
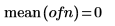
3. 繪製向量數據。
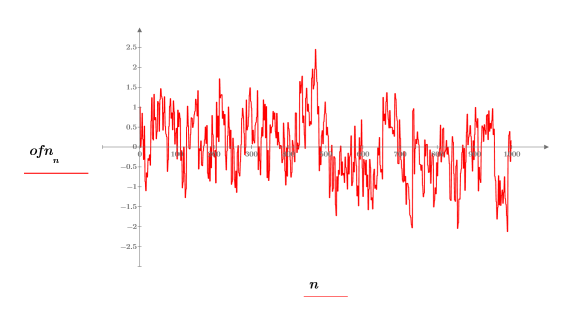
許多自然與人為現象中都可找到 1/f 雜訊,包括音樂、腦波、天氣、股市波動及其他上下階層交互作用的系統。例如,若有人要數位化各種音樂類型的樣本 (搖滾、爵士、古典),他會發現它們的功率頻譜在 1/f 雜訊分佈中非常近似。
4. 使用 lcorr 函數計算兩者的自相關性,以比較此雜訊的統計結構與先前產生的白雜訊。
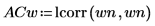
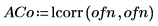
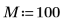
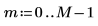
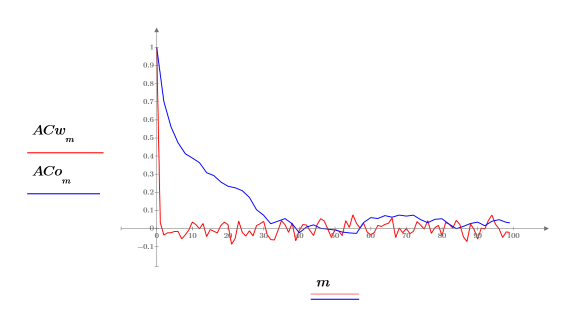
與白雜訊不同的是,onefn 產生的雜訊有相關性,且相關性會隨著延遲增加而衰變。
使用功率頻譜比較雜訊信號
另一種查看白雜訊與 1/f 雜訊差異的方法,是比較其功率頻譜。
1. 假設頻率群組 20 的 50 個柱狀。
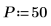
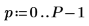
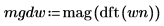
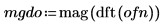
3. 平均頻率群組可使結果平滑。
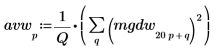
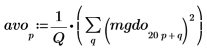
4. 繪製白雜訊頻譜。
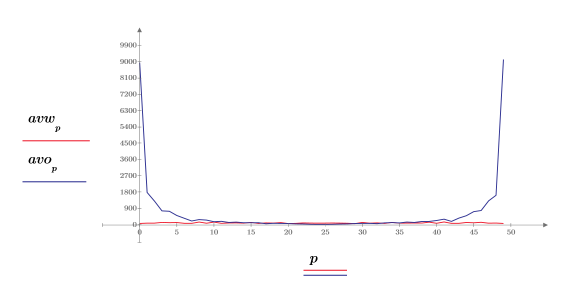
一如預期,白雜訊頻譜基本上是平的。1/f 近似值的量值頻譜,以遞增頻率快速下降。
5. 使用 log 函數計算量值的更具提示性記錄檔。
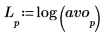
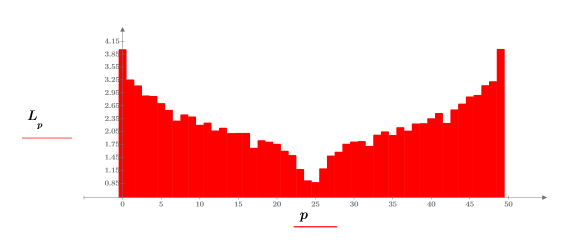
實驗
請嘗試以下實驗:建構 1/f 功率頻譜 (具隨機相角),然後採用逆轉換以取得雜訊向量。
1. 定義頻譜寬度。
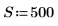
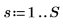
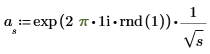
3. 計算後半轉換 (在真實的信號中,後半為中點附近的共軛對稱)。
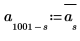
4. 將雜訊均數設定為零。
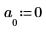
5. 使用 idft 函數取得傅立葉逆轉換 (轉換成時域)。
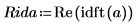
6. 繪製逆轉換的實數值。
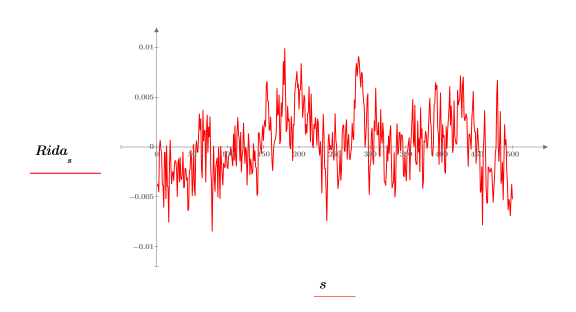
7. 使用 lcorr 函數計算自相關性曲線。
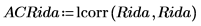
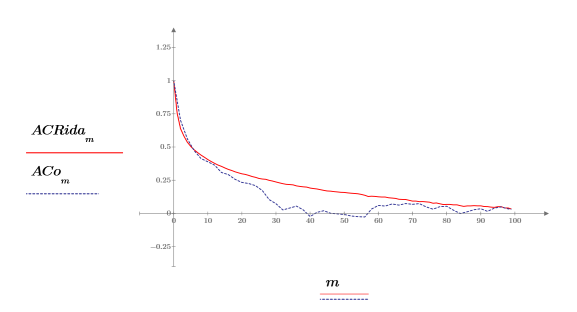
自相關性的行為類似於 onefn 的輸出,在 0 點時具有 1.0 的相關性,在其他點時相關性會發生變化。