範例:相互作用
使用 effects 函數瞭解實驗中相互作用的角色。
1. 使用 fullfact 函數建立兩個係數的設計矩陣。
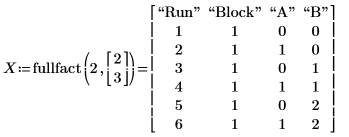
2. 指定矩陣 Vals 中實驗的實數值。性別係數分為兩個級別,男性與女性。年齡係數會分成三個級別:青年、中年及老年。因為係數的級別不同,所以 NaN 會插入 Vals 的第一列,填滿空白元素。
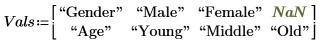
3. 使用 doelabel 函數,以根據性別及年齡對實驗結果進行排序。

矩陣 X 與 D 完全相同,但 X 會顯示係數的編碼值,而 D 則顯示其實數值。
沒有相互作用 - 只有一項顯著因子
1. 記錄各組學習某項工作所消耗的平均時間。對於 Run 1 而言,年輕男性的平均學習時間為 9 分鐘。
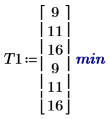
2. 呼叫 effects 函數以檢視性別、年齡及其相互作用的效應。

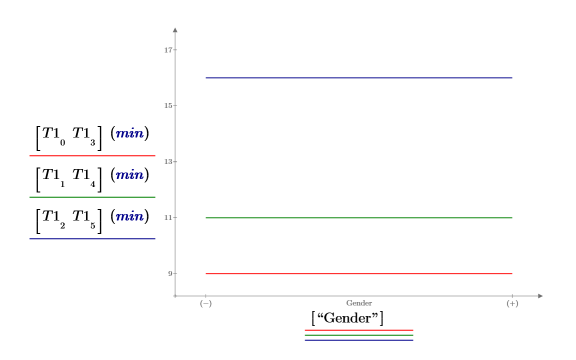
Gender 子矩陣顯示性別不影響學習時間。因此,年齡與性別間無可報告的相互作用效應。
3. 建立效果圖,檢視年齡如何影響學習時間。最年輕一組學習該工作所耗用的平均時間為 9 分鐘。
沒有相互作用 - 兩項顯著因子
1. 記錄各組學習第二項工作所消耗的平均時間。
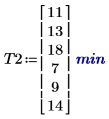
2. 呼叫 effects 函數以檢視性別、年齡及其相互作用的效應。

年齡對學習過程的影響與對第一項工作的影響一樣。但此次,男性學習工作比女性耗用較多的時間。
3. 若要計算不同級別的 A 及 B 之 AB 相互作用效應,請定義 i 及 j 為級別 A 及 B,以及定義 mABi, j 為 AB 在 i 及 j 時的平均回應。

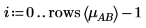
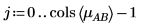
4. 使用 mean 函數計算此實驗的整體均數及每個係數的均數。
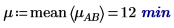
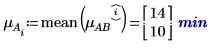
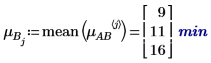
5. 計算每個係數的級別效應。
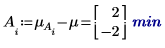
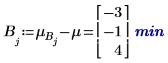
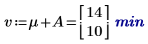
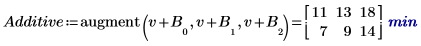
7. 計算 AB 的平均回應以及各級別 A 與 B 的累加係數效應之間的相互作用或差分。
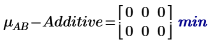
就此項工作而言,年齡與性別之間沒有任何相互作用。
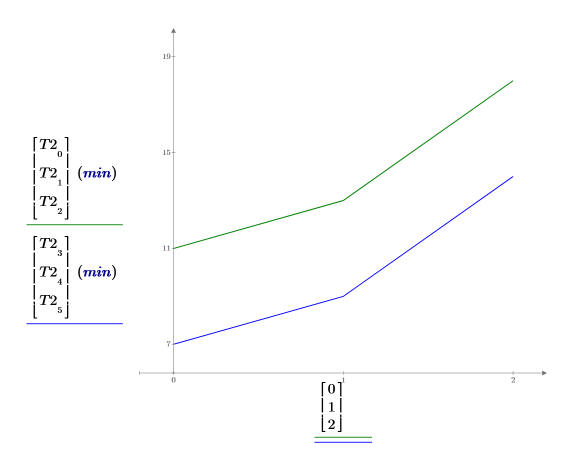
8. 繪製每種性別的平均學習時間。年輕女性學習第二項工作平均需時 7 分鐘。因為性別與年齡之間並無相互作用,所以這兩條曲線是平行的。
有重要的相互作用
1. 記錄各組學習第三項工作所消耗的平均時間。呼叫 effects 函數以檢視性別、年齡及其相互作用的效應。
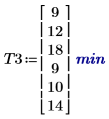

年齡對第一項及第二項工作的影響相同,但性別對第一項工作的影響比第二項工作小。就此第三項工作而言,年齡與性別之間有相互作用。
2. 計算相互作用效應。

3. 使用 mean 函數計算此實驗的整體均數及每個係數的均數。
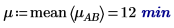
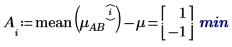
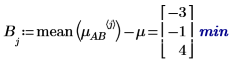
4. 針對係數 A 及 B 的每個級別,使用 augment 函數計算累加係數效應 (整體實驗均數總合)、A 的級別效應,以及 A 及 B 之每個級別的 B 級別效應。
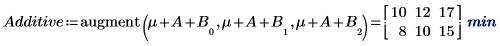
5. 計算 AB 的平均回應以及各級別 A 與 B 的累加係數效應之間的相互作用或差分。
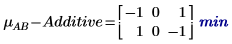
相互作用 AB 的平均回應與累加係數效應之間有差分。
6. 繪製每種性別的平均學習時間。雖然年輕男性與女性的表現毫無差異,但年長男性學會第三項工作需要的時間較女性長。這兩條曲線不平行,因為年齡與性別之間的相互作用相當重要。
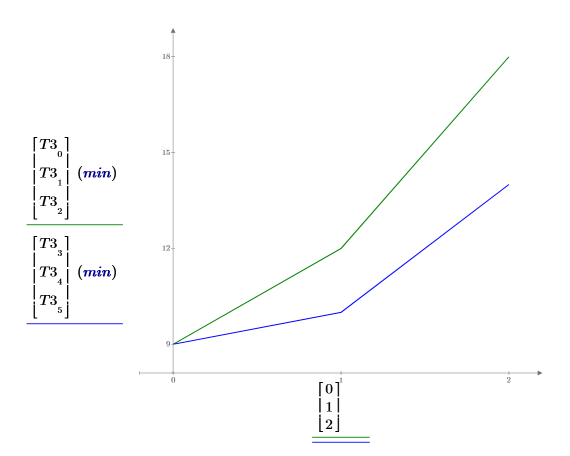
沒有重要的相互作用
1. 記錄各組學習第四項工作所消耗的平均時間。

2. 呼叫 effects 函數以檢視性別、年齡及其相互作用的效應。

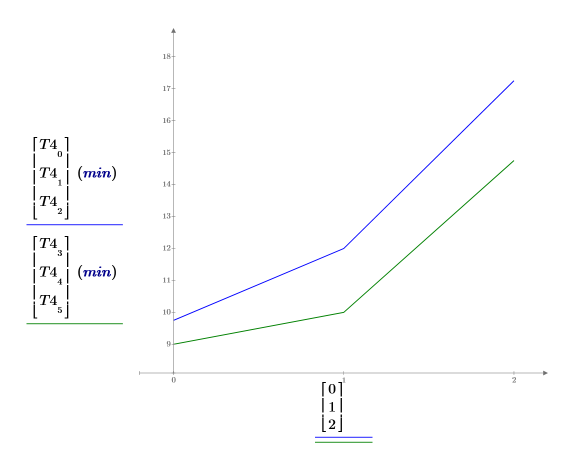
性別與年齡對第三項工作的影響看起來非常相似。
3. 繪製每種性別的平均學習時間。這兩條曲線幾乎平行,表示年齡與性別之間雖有相互作用,但此相互作用並不重要。
參照
著者:J. Neter、M.H. Kutner、C.J. Nachtsheim、W. Wasserman;書刊名:Applied Linear Statistical Models (應用線性統計模型);第 4 版;出版商:McGraw-Hill/Irwin,Boston,1996;頁次:803。