求解 ODE
可使用求解命令块和 odesolve 函数来查找可在给定值范围内满足常微分方程 (ODE) 的函数。
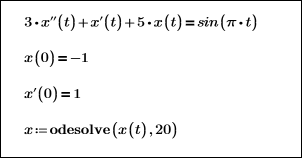
这里,输出函数的求解范围是 0 ≤ x ≤ 20:
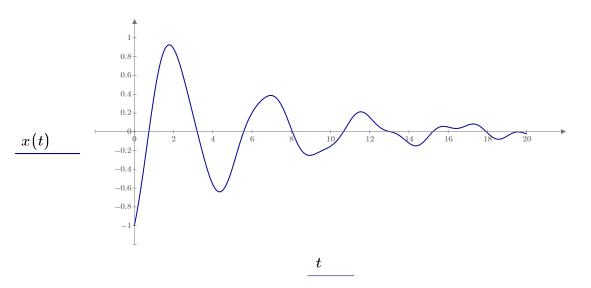
在求解命令块中使用 ODE 时,将应用以下约束:
• 运算符 - 使用“等于”运算符求解 ODE。不要使用比较运算符或不等于运算符。要定义导数,可使用导数或求导运算符,如 d/dx 和 d2/dx2 或 y'(x) 和 y''(x)。
• 初始条件和边界条件 - 对于单个 n 阶 ODE,必须有 n 个独立等式约束:
◦ 初始值问题 - 在单个初始点 a 处要求要有 y(x) 值及它的第一个 n − 1 导数。
◦ 边界值问题 - n 个约束必须指定 y(x) 的某些值及其在初始点 a 或终止点 b 处的导数。约束必须满足 sbval 函数输入的要求。当提供边界值条件时,函数 odesolve 会调用 sbval。
无论何种情况,边界条件中所用的端点必须均与 odesolve 命令中所指定的端点匹配。PTC Mathcad 会检查条件的类型和数量是否正确,如果不正确则会返回错误。
设置初始条件时不支持表示导数的莱布尼茨符号 dy/dx。此时,请使用导数运算符 y’,该符号称为拉格朗日符号。 |
• 代数条件 - 可添加代数条件,例如 y(b) + z(b) = w(b)。求解命令块中包含一个额外的未知函数 w,必须在 odesolve 中将其指定一个输出函数。
• 输出 - 必须将 odesolve 函数的输出分配给某个函数名或由不带自变量的函数名组成的矢量。
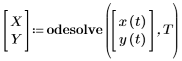
这些函数的隐含参数是积分变量:
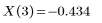
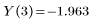
求解方法
• 根据问题的规模,以及所使用的相对步长大小,可能需要减小 TOL 的值以获得合适的解。当 PTC Mathcad odesolve 报告积分步骤过多时,可尝试此方法。
• 正在求解的函数在积分区间内不得包含任何奇点。否则,它们可能会产生不可靠的结果。
• 在求解多循环的周期行为问题时,可能会出现混淆。若要在结果中得到预期频率,可增加插值点的数量。
• 若要求解最高导数项中的非线性 ODE 或求解程序循环中的 ODE,可使用 rkfixed 或其中一个其他命令行 ODE 求解器。还可在使用本地函数的程序循环中分配某个参数化求解命令块的输出。