奇异值分解
• svds(A) - 返回包含 A 的奇异值、矩阵 AH·A 的 eigenvalues 的正平方根的矢量 (其中 AH 为 A 的共轭转置)。可使用 transpose 和 complex conjugate 运算符计算 AH,如下所示。
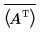
• svd(A) - 返回一个由 3 个嵌套数组组成的矢量。
第一个数组包含由 svds 返回的奇异值组成的矢量 s。接下来的两个数组为矩阵 U 和 VH,满足 A = U∙diag(s)·VH。第三个条目 VH 为 V 的共轭转置。
第三个数组为 VH 而非 V。这意味着共轭转置已应用至返回的数组。无需再次应用它。可以在公式中直接使用返回的数组。
自变量
• A 为 m × n 数组,其中 m ≥ n。对于 svd,数组元素必须为实数;对于 svds,允许复数值。
附加信息
• 奇异值始终为实数并且为正。极小值应解释为 0。
• svd 函数采用 Intel 基本线性代数子程序 (BLAS)/线性代数程序包 (LAPACK) 库。