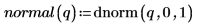示例：数据矢量的 Z 值

函数 > 统计 > 概率分布 > 示例：数据矢量的 Z 值

示例：数据矢量的 Z 值

计算正态分布数据矢量的 Z 值，其中总体标准差为已知。

1. 定义要分析的数据集。

2. 计算样本的平均值 m_s。

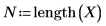
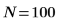
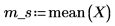
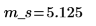
3. 定义显著性水平、总体标准差和建议使用的总体均值。

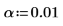
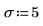
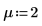
4. 计算 z 值。

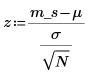
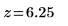
5. 为双尾检验指定虚假设和备择假设。

H0: m = μ

H1: m ≠ μ

6. 使用 pnorm 函数计算 p 值并检验假设。在本例中，当原假设为真 (不拒绝 H0) 时，所有布尔表达式的计算值均为 1。

<region id="ID0EA35BB" top="883.20000000000016" left="38.400000000000006" height="25.6" width="185.36333333333334" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="84">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">P</id>
      <apply>
        <mult />
        <real>2</real>
        <parens>
          <apply>
            <minus />
            <real>1</real>
            <apply>
              <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">pnorm</id>
              <sequence>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">z</id>
                <real>0</real>
                <real>1</real>
              </sequence>
            </apply>
          </apply>
        </parens>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

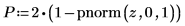
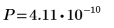
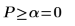
假设原假设为真，检验统计大于观察值的概率为 4.11*10-10。p 值与显著性水平之间的比较结果显示：有证据表明备择假设为真。

7. 使用 qnorm 函数计算临界区的极限并检验假设。

<region id="ID0EO65BB" top="1171.2000000000003" left="38.400000000000006" height="47.2" width="163.91666666666669" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="90">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">crit</id>
      <apply>
        <absval />
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">qnorm</id>
          <sequence>
            <apply>
              <div />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">α</id>
              <real>2</real>
            </apply>
            <real>0</real>
            <real>1</real>
          </sequence>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

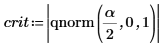
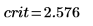
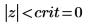
拒绝原假设。很明显平均值不等于 μ。

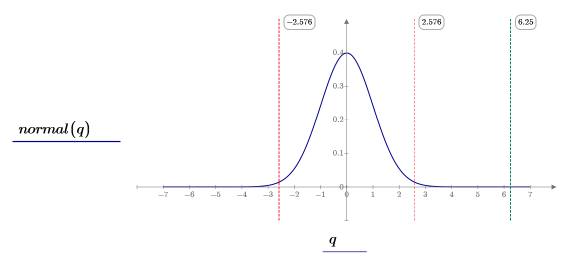
8. 使用 dnorm 函数计算和绘制标准正态分布 (蓝色)、临界区域的边界 (红色) 和 z 值 (绿色)。

<region id="ID0EYC6BB" top="1382.4" left="38.400000000000006" height="25.6" width="196.62333333333334" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="96">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="VARIABLE" xml:space="preserve">normal</id>
        <boundVars>
          <id labels="VARIABLE" xml:space="preserve">q</id>
        </boundVars>
      </function>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">dnorm</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">q</id>
          <real>0</real>
          <real>1</real>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>