示例:小波变换
使用小波变换函数来压缩数据。
1. 定义一个单独的方波信号,其中:
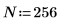
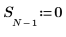
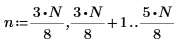
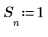
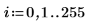
2. 计算数组 n,并绘制信号 S 的图像:

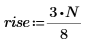
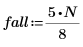
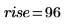
在 0-255 范围以外,信号 S 的振幅对所有 n (96-160) 值均为 1,否则振幅为 0。
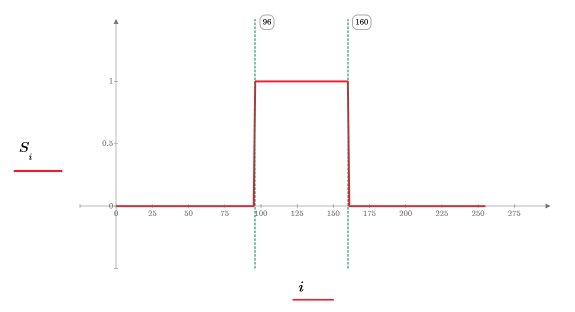
3. 使用波函数来计算信号 S 的小波变换:
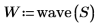
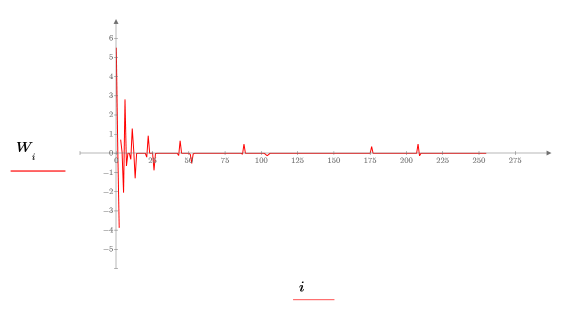
4. 计算此变换中包含的阶数:
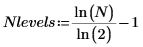
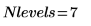
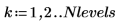
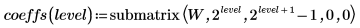
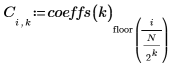
6. 同时绘制多阶系数:
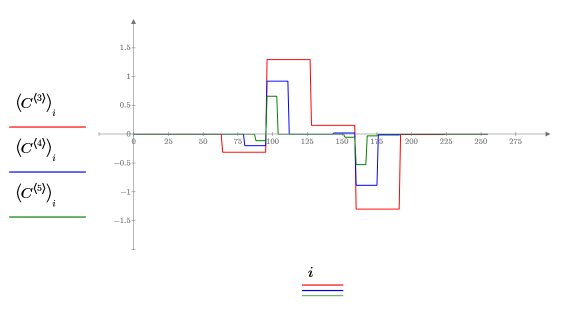
7. 通过执行下面两个操作,可用较少的数据表示信号:
a. 将更高阶系数归零
b. 计算新系数矢量的逆小波变换
系数被设为零的第一阶 (L < 7 可能会有所变化)。
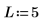
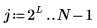
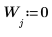
8. 使用函数 iwave 恢复原始信号:
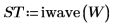
9. 绘制并比较原始信号与已变换的信号:
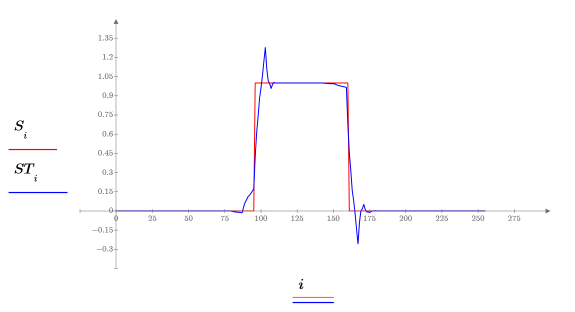
此方法可压缩表示信号所需的数据。