示例:方程的符号解
以符号形式求解有一个或多个未知量的方程。
求解单个方程
1. 键入下面的方程:
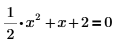
2. 插入符号运算符,在占位符中键入关键字 solve,并按 Enter。
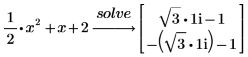
由于方程的右侧为 0,您无需键入表达式的 =0 部分。 |
3. 以小数格式将常数 2 键入为 2.0,从而以浮点格式返回答案。
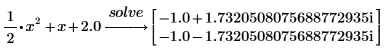
4. 求解具有一个变量的方程。
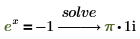
5. 求解具有多个变量的方程。
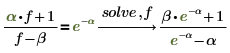
当方程包含多个变量时,您必须指定要求解的变量。 |
6. 求解四阶多项式。

以上结果显示四阶多项式的符号解得到四个数值解。 |
7. 使用参数化系数查找多项式方根。
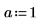
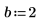
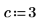
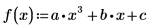
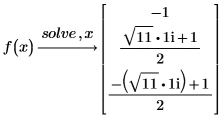
求解方程组和等式组
可将多个方程和等式合成一个矢量,进而以方程组形式对它们进行求解。
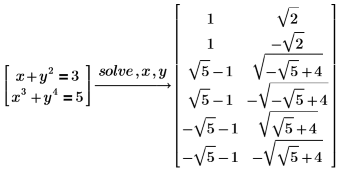
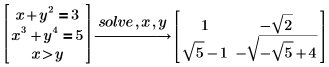
以根求解多项式
默认情况下,PTC Mathcad 求解最大为 4 次根的多项式方程。使用普通算术运算,以根的形式构建解。
1. 求解以下多项式:
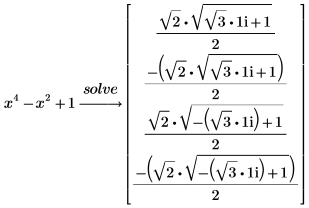
数学家伽罗瓦在 19 世纪证明了存在 5 次的多项式,如果高于该次数将无法以根求解。对于这些多项式,PTC Mathcad 会返回方根的数值近似值。 |
2. 求解 5 次多项式。

以上结果显示五阶多项式的符号解得到五个数值解。 |
进行有关变量域的假设
使用关键字 assume 来进行有关问题中变量域的假设,例如假设其为实数。
1. 求解假设 x 为实数的方程。
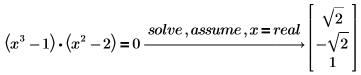
PTC Mathcad 只返回方程的实数解。 |
2. 使用 RealRange 在值域 (0, 2) 中求实数解。
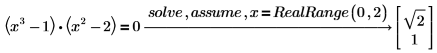
3. 键入 x=integer 只求整数解。
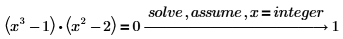
4. 使用 assume 在符号运算中限制变量的域。
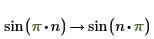
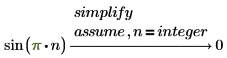
返回方程的详细解
在 solve 后添加修饰符 fully 来返回方程的详细解。
1. 使用函数 clear.sym 来清除 a 先前的符号值。
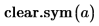
2. 使用 fully 返回 a 的值,解对其有效。
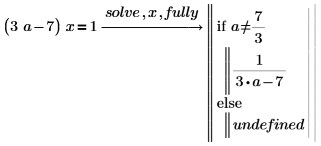
3. 使用详细结果来定义函数。
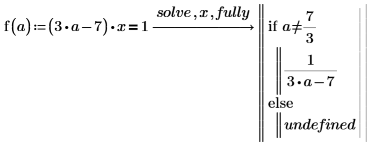
4. 在 a=3 和 a=7/3 时计算函数:
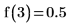
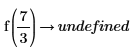
具有周期解的方程
对于解为周期性解的方程,PTC Mathcad 会返回单个解,后接一个表达式,用于在第一个解中添加周期的整数倍。
1. 使用 fully 来计算 sin(x)。
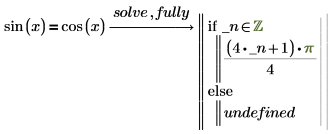
If 语句后的表达式表示 pi/4 加上 pi 的所有整数倍数。PTC Mathcad 会插入新生成的变量 _n,其表示任意整数。在生成的变量前添加下划线,避免名称与在工作表别处定义的其他变量冲突。 |
2. 添加修饰符 using,后接使用布尔型等号写下的方程,将生成的变量设置为等于新变量。
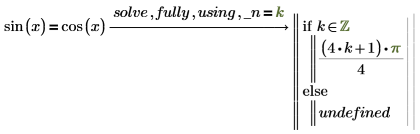
如果您在 using 后面指定的变量并非 solve 将要返回的生成变量,PTC Mathcad 会返回一个错误。