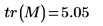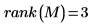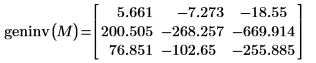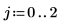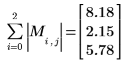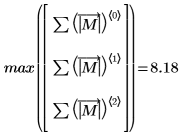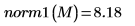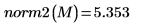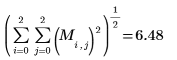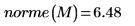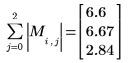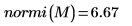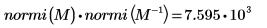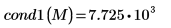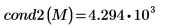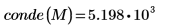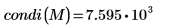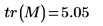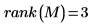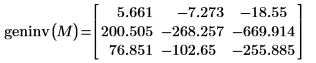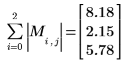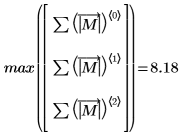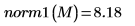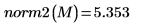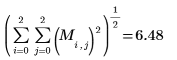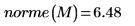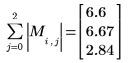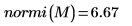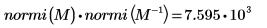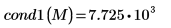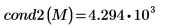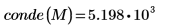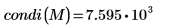示例：矩阵的特殊特征

矢量、矩阵和表格 > 使用数组 > 示例：矩阵的特殊特征

示例：矩阵的特殊特征

求出方阵的迹、秩、广义逆、范数和条件数。

矩阵的迹、秩和广义逆

1. 使用 tr 函数求出 M 的迹或对角线元素之和。

2. 使用 rank 函数求出实值矩阵 M 的秩。

3. 使用 geninv 函数求出矩阵 M 的广义逆。

矩阵的不同范数

1. 求出 M 的 L1 范数，并将结果与函数 norm1 的输出进行比较

L1 范数是列绝对值之和的最大值 (j=0, 1, 2 所得的最大值)。

单击可复制此表达式

<region id="ID0EDGOHB" top="1056.0000000000002" left="19.200000000000003" height="136.00000000000003" width="191.66000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="53">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">max</id>
        <matrix rows="3" cols="1">
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>0</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>1</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <id xml:space="preserve">M</id>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
        </matrix>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
  </math>
</region>

2. 使用 norm2 函数求出 M 的 L2 范数。

3. 使用 norme 函数求出 M 的欧几里得范数：

矩阵的欧几里得范数与矢量的欧几里得范数相似：

<region id="ID0EFLOHB" top="1440.0000000000002" left="38.400000000000006" height="60.441333557128914" width="176.66000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="59">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <pow />
        <parens>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id xml:space="preserve">i</id>
              </boundVars>
              <apply>
                <summation />
                <lambda>
                  <boundVars>
                    <id xml:space="preserve">j</id>
                  </boundVars>
                  <apply>
                    <pow />
                    <parens>
                      <apply>
                        <indexer />
                        <id xml:space="preserve">M</id>
                        <sequence>
                          <id xml:space="preserve">i</id>
                          <id xml:space="preserve">j</id>
                        </sequence>
                      </apply>
                    </parens>
                    <real>2</real>
                  </apply>
                </lambda>
                <lowerBound>
                  <real>0</real>
                </lowerBound>
                <upperBound>
                  <real>2</real>
                </upperBound>
              </apply>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <real>2</real>
            </upperBound>
          </apply>
        </parens>
        <apply>
          <div />
          <real>1</real>
          <real>2</real>
        </apply>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
  </math>
</region>

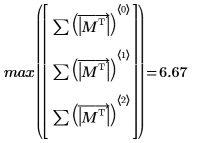
4. 求出 M 的无穷范数，并将结果与函数 normi 的输出进行比较。

无穷范数是行绝对值之和的最大值 (i=0, 1, 2 所得的最大值)

单击可复制此表达式

<region id="ID0ELOOHB" top="1766.4000000000003" left="19.200000000000003" height="143.056" width="200.52000000000004" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="65">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve">max</id>
        <matrix rows="3" cols="1">
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <apply>
                        <transpose />
                        <id xml:space="preserve">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real>0</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <apply>
                        <transpose />
                        <id xml:space="preserve">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real>1</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <placeholder />
              </boundVars>
              <apply>
                <matcol />
                <parens>
                  <apply>
                    <vectorize />
                    <apply>
                      <absval />
                      <apply>
                        <transpose />
                        <id xml:space="preserve">M</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
                <real>2</real>
              </apply>
            </lambda>
            <upperBound>
              <placeholder />
            </upperBound>
          </apply>
        </matrix>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
  </math>
</region>

矩阵的不同条件数

矩阵的条件数是两个矩阵范数的乘积。它可测量线性方程组的解对输入矢量中错误的敏感度。

1. 使用 cond1 函数求出 M 的 L1 条件数。

2. 使用 cond2 函数求出 M 的 L2 条件数。

3. 使用 conde 函数求出 M 的欧几里得条件数。

4. 使用 condi 函数求出 M 的无穷条件数。

相关主题

关于使用数组

这对您有帮助吗?