示例:信号窗口化
使用下列函数执行信号窗口化:
理想低通脉冲响应/截断的低通脉冲响应
1. 以正则化的截断频率 0.15 定义理想低通滤波器的脉冲响应 h。
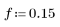
2. 定义脉冲响应。
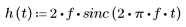
由于可实现的有限长度的滤波器一定具有有限的脉冲响应,所以此理想响应会被截断为一些可以管理的项数。
3. 要检查不经过窗口化直接截断对频率响应的影响,可定义只包含理想响应的中央 N 项的长度为 N 的滤波器,经过偏移获得因果滤波器。
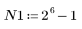
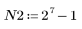
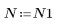
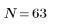
作为练习,将 N 设置为 N2 并观察下面示例中项数增加时的影响。
4. 在各项范围上应用脉冲响应函数并绘制结果函数。
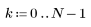
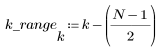
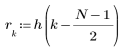
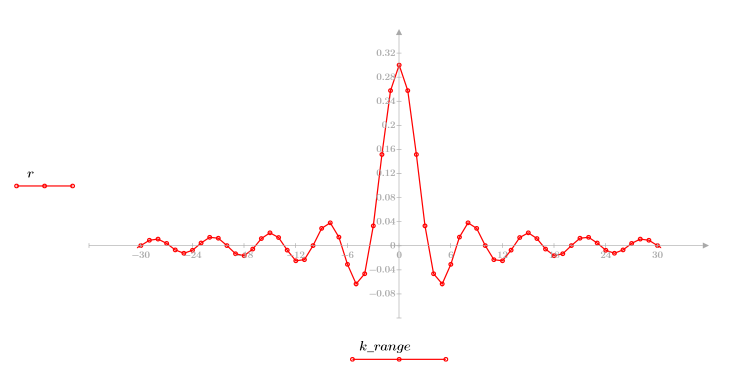
5. 使用 gain 函数计算此截断信号的频率响应,但首先要定义频率范围 (多个样本频率)。
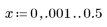
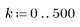
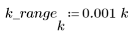
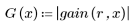
6. 将 gain 函数的离散量收集到新的数组中。
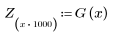
7. 查找 G 的最大幅度及其相应的频率。
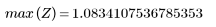
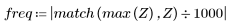
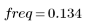
当项数为 N1=63 时,在频率 freq=0.134 位置处会出现最大增益 1.083。
当项数为 N2=127 时,在频率 freq=0.142 位置处会出现最大增益 1.092,从而更接近频带边界。
在频率 freq=0.2 位置处,增益几乎会减小为零。比较以下所有示例中此频率附近的增益。
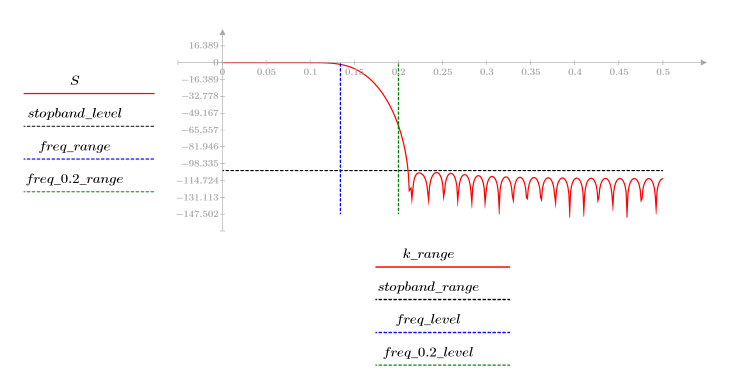
8. 在已定义范围内绘制 gain 函数并显示幅度最大时对应的频率。
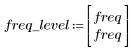
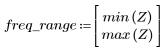
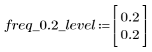
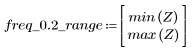
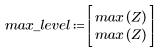
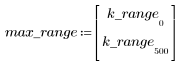
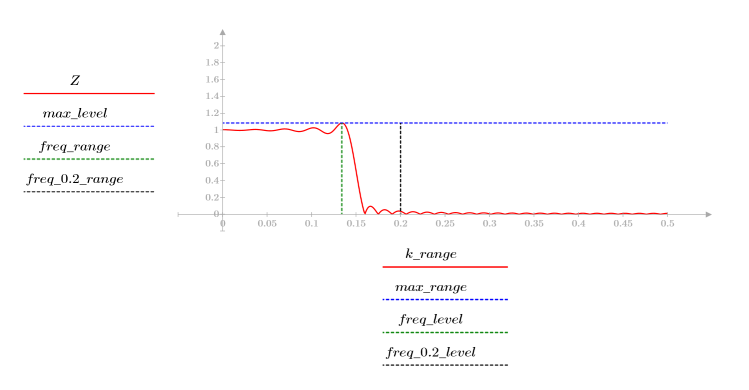
在通频带边界发生超调被称为吉布斯现象。将滤波器阶数 N 从 N1=63 增加到上述的 N2=127,会使超调更接近频带边界,但不会减小其振幅。
从 1 过渡为 0 的波形会随滤波器阶数值 N 的增加而变得更尖。
生成更多所需频率响应的一种方式是窗口化理想脉冲响应,以便在滤波器脉冲响应的边界处可以更加平滑地过渡到 0。将窗口逐项与响应矢量 r 相乘。
三角窗
函数 triangular 返回宽度为 N 的三角窗或 Bartlett 窗。
结果矢量第 j 个元素的计算方法:
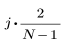
对于
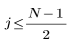
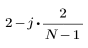
对于
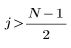
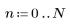
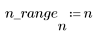
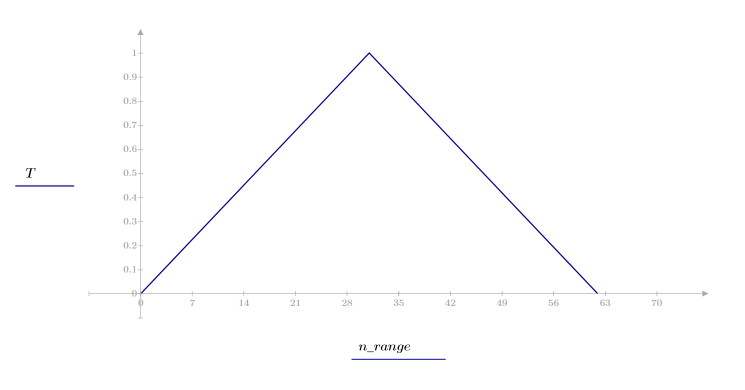
1. 将该函数应用于滤波器阶数 N 并绘制结果矢量图像。
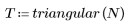
2. 计算窗口化的脉冲响应。
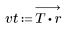
3. 使用 gain 函数计算和绘制此滤波器在频率为 k/1000 时的增益,单位为 dB,系数为 vt。
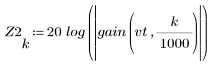
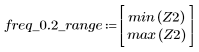
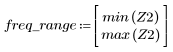
汉宁窗
函数 hanning 返回宽度为 N 的汉宁窗。
结果矢量第 k 个元素的计算方法:
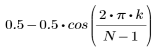
1. 将该函数应用于滤波器阶数 N 并绘制结果矢量图像。
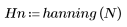
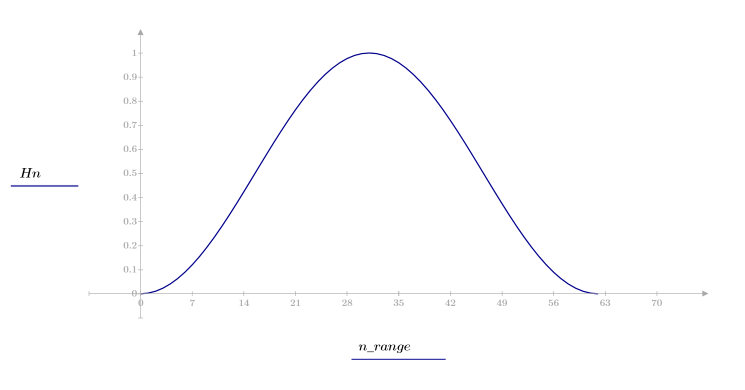
2. 计算窗口化的脉冲响应。
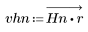
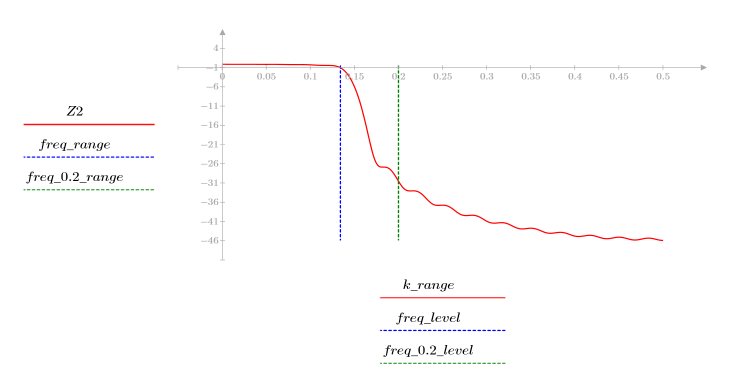
3. 使用 gain 函数计算和绘制此滤波器在频率为 k/1000 时的增益,单位为 dB,系数为 vhn。
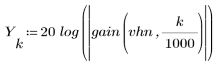
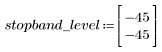
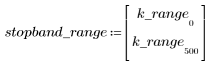
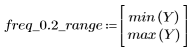
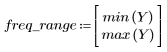
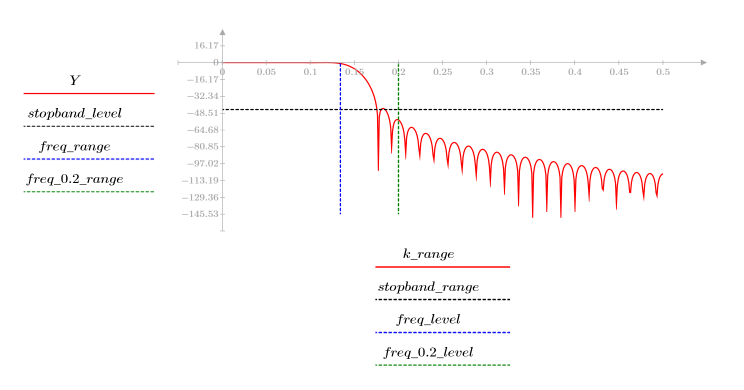
阻带波纹约为 -45 dB。
汉明窗
函数 hamming 返回宽度为 N 的汉明窗。
结果矢量第 k 个元素的计算方法:
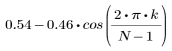
1. 将该函数应用于滤波器阶数 N 并绘制结果矢量图像。
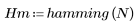
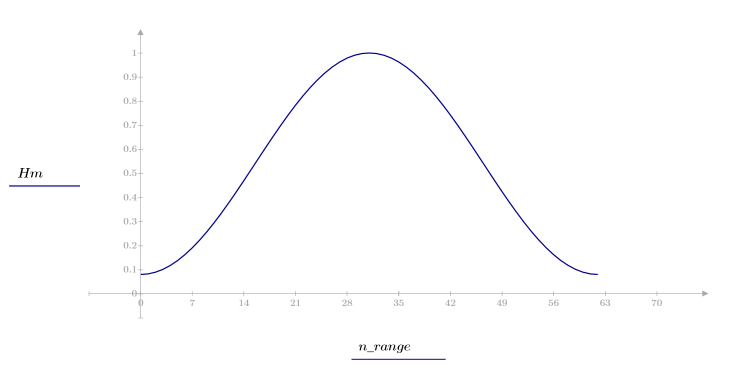
2. 计算窗口化的脉冲响应。
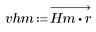
3. 使用 gain 函数计算和绘制此滤波器在频率为 k/1000 时的增益,单位为 dB,系数为 vhm。
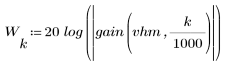
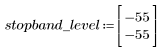
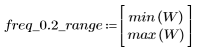
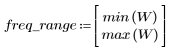
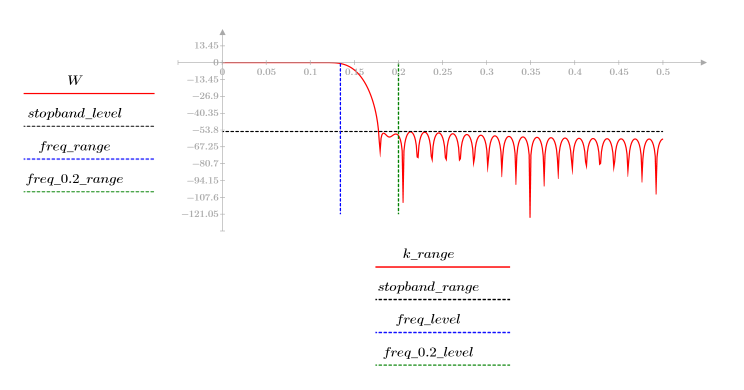
阻带波纹约为 -55 dB。
布拉克曼窗
函数 blackman 返回宽度为 N 的布拉克曼窗。
结果矢量第 k 个元素的计算方法:
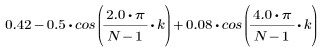
1. 将该函数应用于滤波器阶数 N 并绘制结果矢量图像
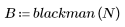
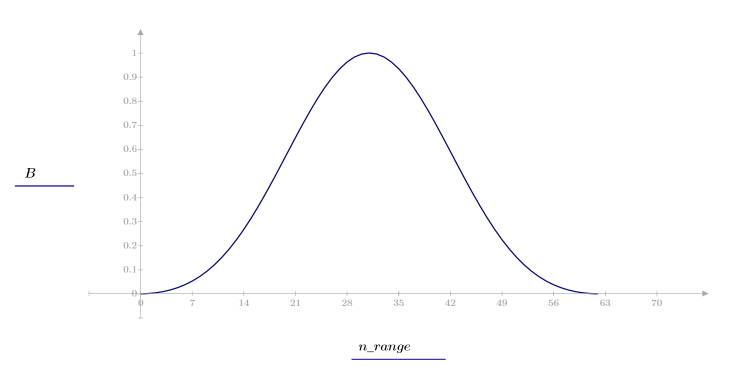
2. 计算窗口化的脉冲响应。
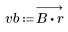
3. 使用 gain 函数计算和绘制此滤波器在频率为 k/1000 时的增益,单位为 dB,系数为 vb。
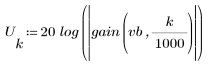
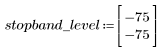
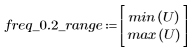
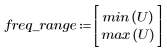
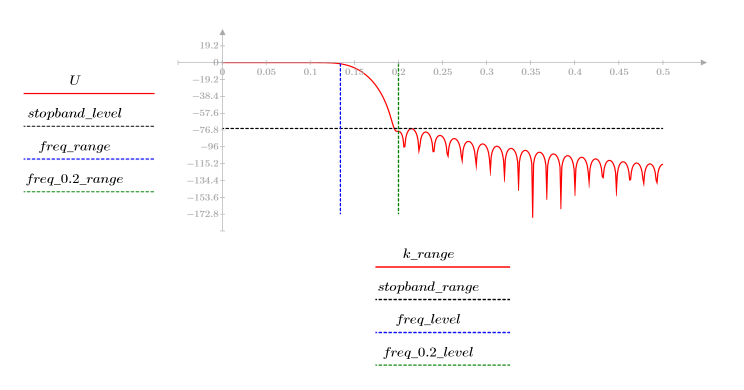
阻带波纹约为 -75 dB。
Nuttall 窗
函数 nuttall 返回宽度为 N 的 Nuttall 窗。
结果矢量第 k 个元素的计算方法:
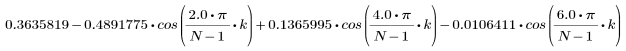
1. 将该函数应用于滤波器阶数 N 并绘制结果矢量图像。
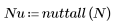
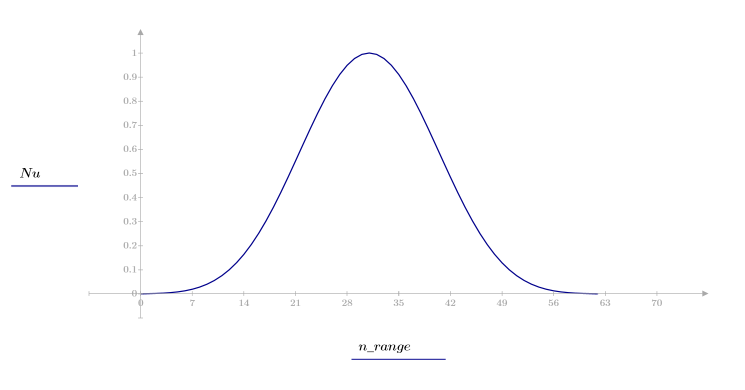
2. 计算窗口化的脉冲响应。
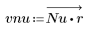
3. 使用 gain 函数计算和绘制此滤波器在频率为 k/1000 时的增益,单位为 dB,系数为 vnu。
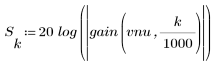
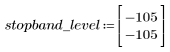
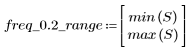
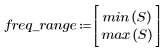
阻带波纹约为 -105 dB。
尖顶矩形窗
函数 taprect 返回宽度为 N 的尖顶矩形窗。
此窗口中部水平高度为 1,渐缩的两端为余弦曲线形式。右侧和左侧均使用下列值:
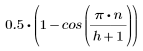
其中
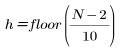
且 n 的范围为从 0 到 h。
1. 将该函数应用于滤波器阶数 N 并绘制结果矢量图像。
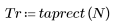
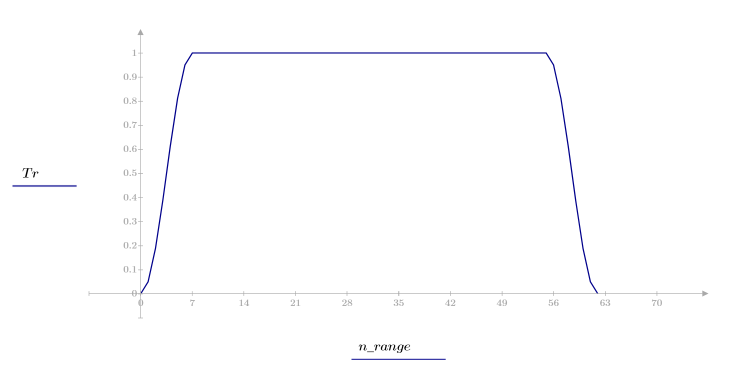
2. 计算窗口化的脉冲响应。
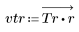
3. 使用 gain 函数计算和绘制此滤波器在频率为 k/1000 时的增益,单位为 dB,系数为 vtr。
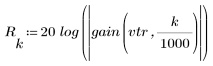
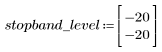
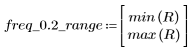
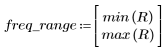
高斯窗
函数 gaussian 返回宽度为 N、参数为 a 的高斯窗。其中参数 a 是与高斯方差逆变换成正比的实数,且必须满足 2 < a < 20。
结果矢量第 k 个元素的计算方法:
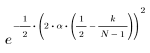
1. 将该函数应用于滤波器阶数 N 并绘制结果矢量图像。
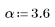
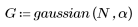
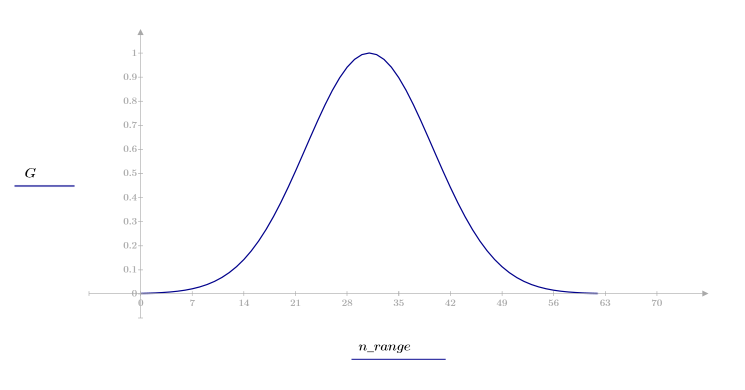
2. 计算窗口化的脉冲响应。
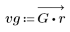
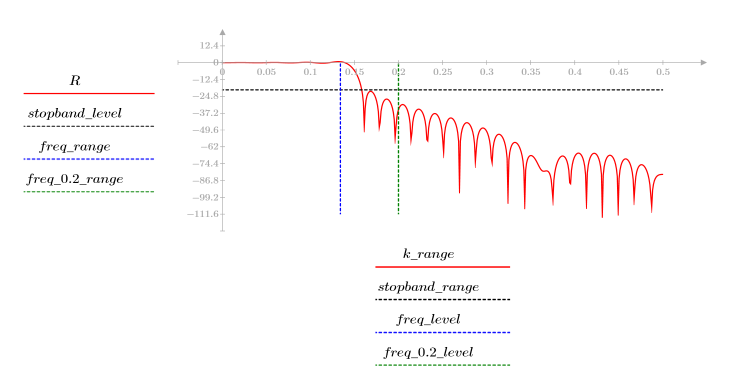
3. 使用 gain 函数计算和绘制此滤波器在频率为 k/1000 时的增益,单位为 dB,系数为 vg。
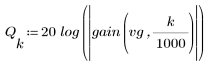
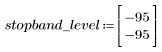
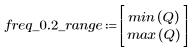
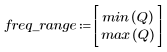
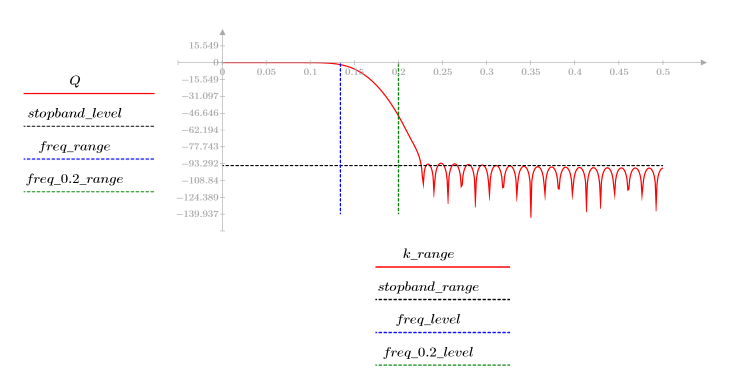
阻带波纹约为 -95 dB。
凯泽窗
函数 kaiser 返回宽度为 N、参数为 b 的凯泽窗。参数 b 必须满足 2≤b≤20。
结果矢量第 k 个元素的计算方法:
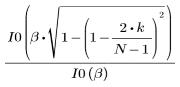
1. 将该函数应用于滤波器阶数 N 并绘制结果矢量图像。
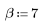
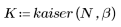
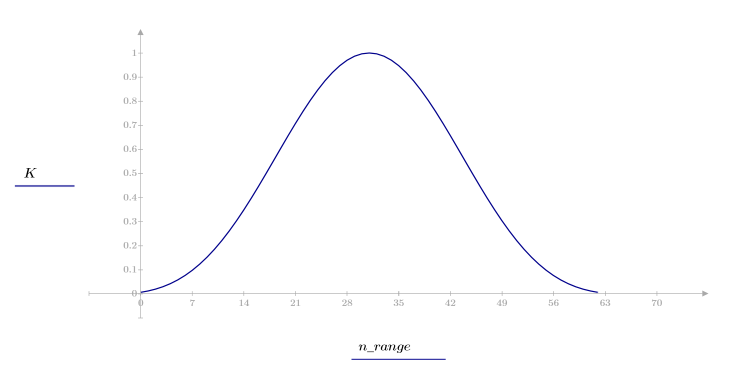
2. 计算窗口化的脉冲响应。
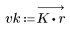
3. 使用 gain 函数计算和绘制此滤波器在频率为 k/1000 时的增益,单位为 dB,系数为 vk。
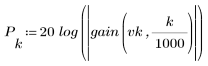
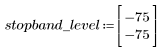
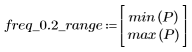
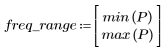
阻带波纹约为 -75 dB。
切比雪夫窗
函数 cheby 返回宽度为 N、参数为 b 的切比雪夫窗或等波纹窗。参数 b 指定最大边波瓣波纹,单位为 dB 且必须满足 b > 1;通常情况下 b > 50。此窗口的长度必须为奇数。切比雪夫窗通过对在单位圆周围的点上计算的切比雪夫多项式进行离散傅立叶逆变换加以计算。有关此窗口的更多信息,请参见 Programs for Digital Signal Processing (《数字信号处理的程序》) (IEEE Press)。
1. 将该函数应用于滤波器阶数 N 并绘制结果矢量图像。
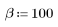
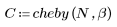
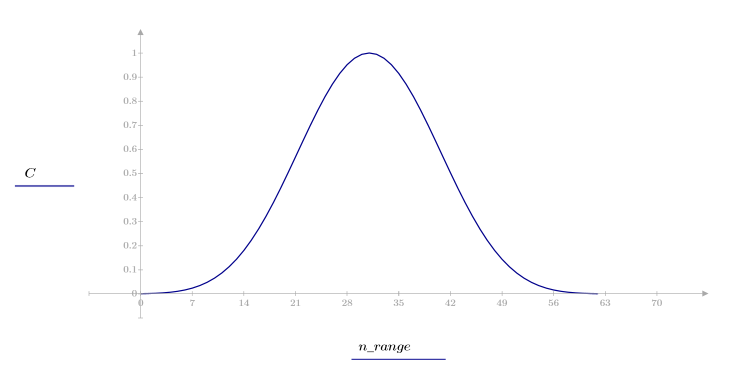
2. 计算窗口化的脉冲响应。
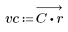
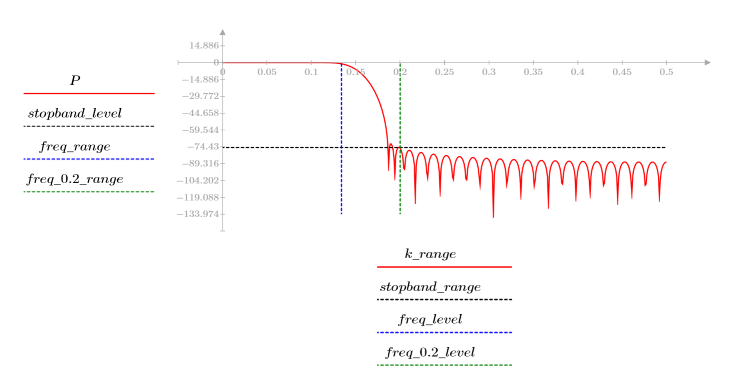
3. 使用 gain 函数计算和绘制此滤波器在频率为 k/1000 时的增益,单位为 dB,系数为 vc。
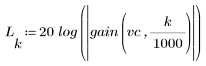
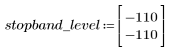
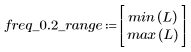
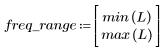
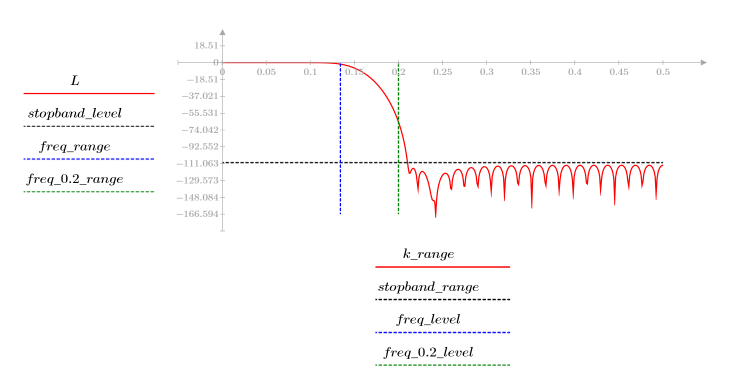
阻带波纹约为 -110 dB。
取余弦窗
函数 costaper 类似于函数 taprect,可返回尾部渐缩的余弦曲线形式的矩形窗。但是,前者可以使用参数 a 指定应通过余弦曲线创建的窗口的百分比。参数 a 应介于 0 和 1 之间;a 的值为 0 时会返回矩形窗口,而 a 的值为 1 时会返回递增余弦曲线窗口。
对于窗口的渐缩部分,第 k 个元素的值计算方法如下:
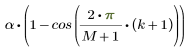
其中,M 是落在其中一个尾部的窗口元素的数量,通过 a-N 计算得出:
1. 将该函数应用于滤波器阶数 N 并绘制结果矢量图像。
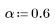
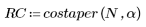
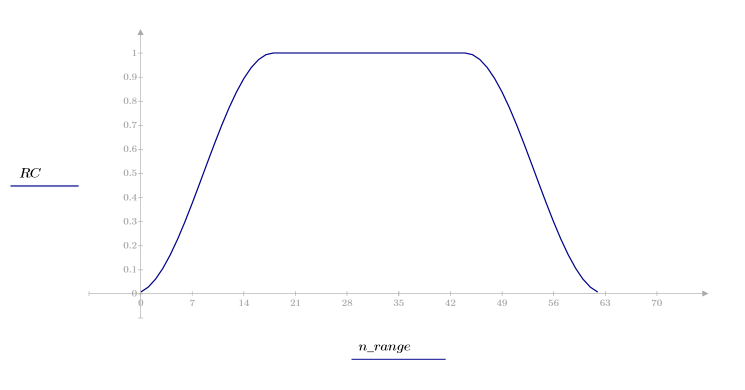
2. 计算窗口化的脉冲响应。
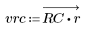
3. 使用 gain 函数计算和绘制此滤波器在频率为 k/1000 时的增益,单位为 dB,系数为 vrc。
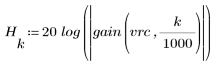
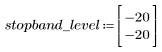
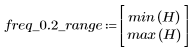
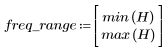
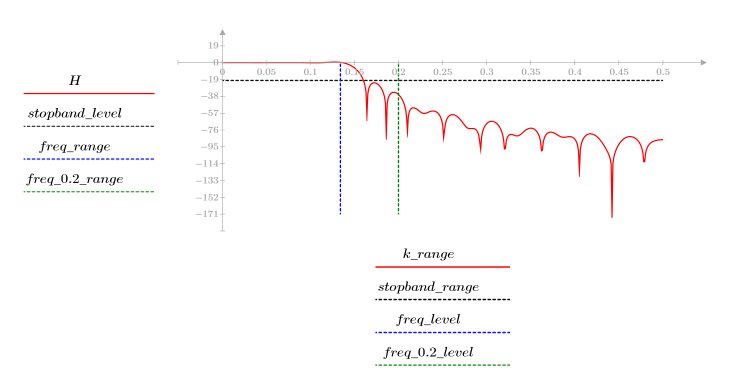
阻带波纹约为 -20 dB。
参考资料
• S. Lawrence Marple, Jr., Digital Spectral Analysis with Applications, Prentice-Hall (1987).
• Lawrence R. Rabiner and Bernard Gold, Theory and Application of Digital Signal Processing, Prentice-Hall, Inc. (1975).
• T. W. Parks and C. S. Burrus, Digital Filter Design, Wiley-Interscience (1987).