示例:残差分析
计算数据集的残差以检查该数据集是否为线性分布。在将回归模型用于预测之前,检查已满足下列线性模型假设:
• 误差不相关。
• 对于 X 的任何给定值,误差应符合均值为零且方差为常量的正态分布。
标准化残差
要解释残差的相对量,可以对残差进行标准化。需要用残差除以误差标准差的估值。
1. 定义下列数据集:
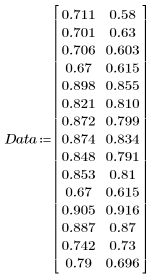
2. 绘制数据集图像。
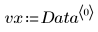
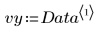
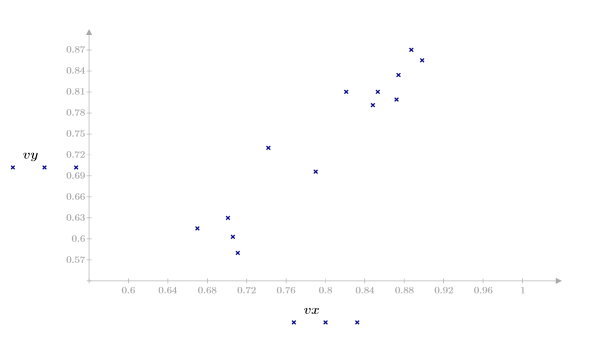
数据看起来是线性的。这通过接近 1 的相关系数来确认:
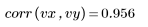
3. 定义最佳拟合线:
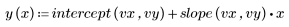
4. 从测量值减去拟合值。
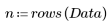
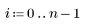
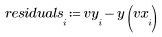
5. 用残差除以估计的标准误差。
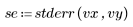
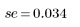
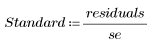
学生化残差
学生化残差或调整的标准化残差是标准误差的另一种常用估值。此估值将针对每个 x 值和 x 的均值之间的距离进行调整。
1. 计算每个值与均值间的距离。
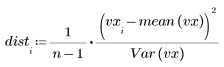
2. 定义每个残差要利用的标准差。

3. 定义学生化残差:
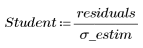
学生化残差比标准化残差更精确,因其说明了误差方差中的任何点到点的差异。尽管如此,这两种残差在值上通常是相近的:
 |  |
4. 调用 polyfitstat。显示包含学生化残差的观察诊断的子矩阵。
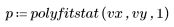
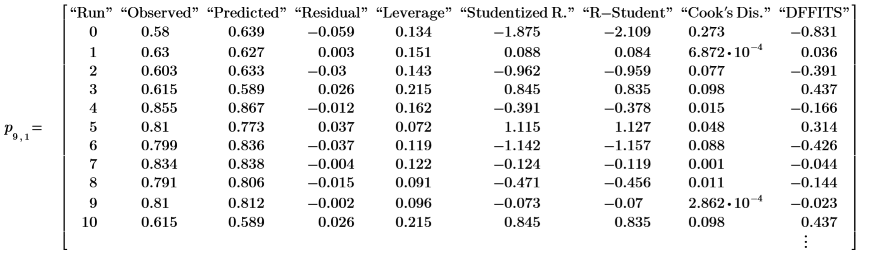
检查线性
检查 Data 集为线性相关的。利用具有曲线关系的随机样本创建一个对照示例。如果数据为线性相关,并且误差为正态分布,则散点图没有可辨别的图形。点随机分散在假设的误差均值零的周围。
1. 针对 x 值和预测的 y 值绘制残差图像。
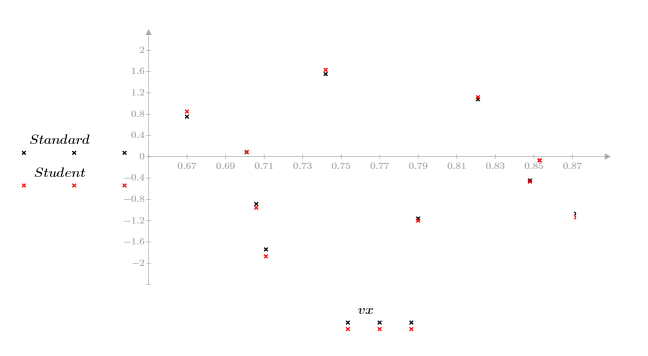
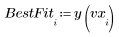
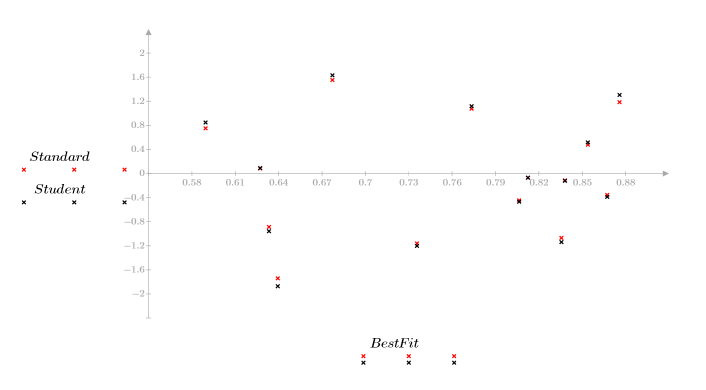
无残差图形表示数据为线性相关。
2. 生成具有二次关系的点的随机样本。
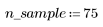
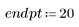
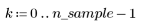
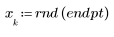
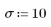
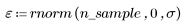
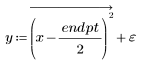
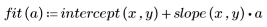
3. 绘制残差相对量的图像。
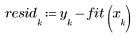
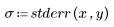
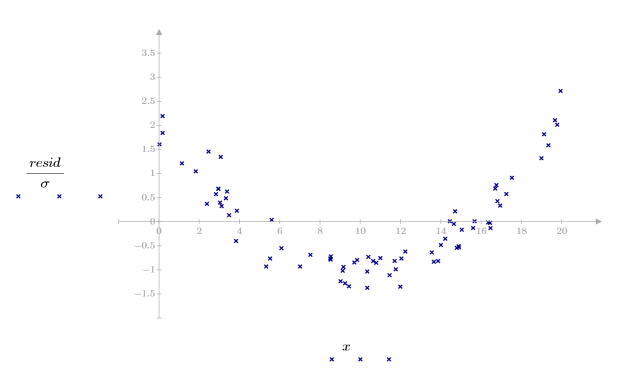
数据中的二次图形反映在残差的散点图中。此数据为非线性相关。
检查常量误差方差
Data 集中未检测到误差方差图形。创建一个对照示例,其中数据显示为线性但误差方差为非正态分布,同时残差的散点图从左到右显示递增或递减分散。
1. 生成从左到右递增分散的点的随机样本。
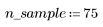
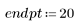
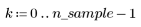
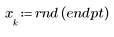
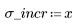
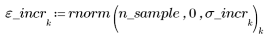
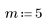
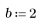
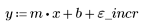
2. 计算最佳拟合线。绘制随机数据集和拟合函数的图像。
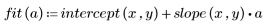
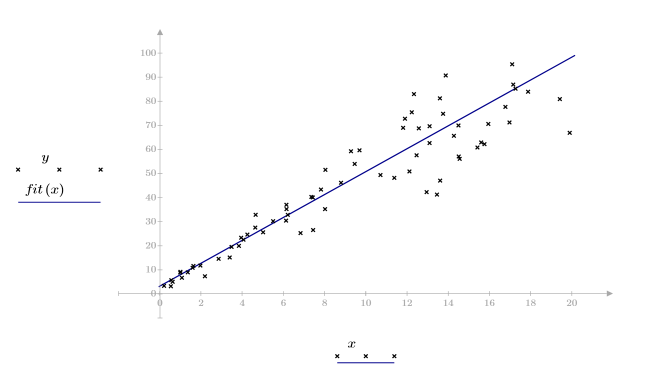
相关系数接近 1,表示该数据为线性相关:
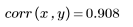
3. 绘制残差相对量的图像。
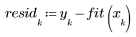
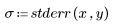
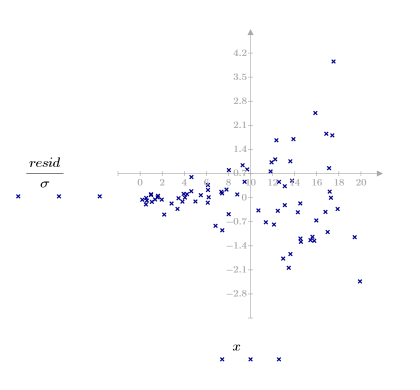
残差的散点图显示不随机分布。残差图中的点从左到右递增分散。
检查误差的相关性
可通过利用 Durbin-Watson 统计检查线性回归模型中的相邻误差项是否相关。
计算 Data 集的 Durbin-Watson 统计量:
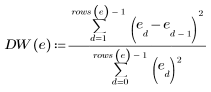
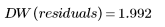
Durbin-Watson 统计量的值域为 0 到 4。如果相邻项不相关,则 Durbin-Watson 值接近 2。小于 2 的 Durbin-Watson 值表示正相邻相关,而大于 2 的 Durbin-Watson 值则表示负相邻相关。
Durbin-Watson 统计用于最小二乘 B 样条的计算。遗憾的是,Durbin-Watson 统计无法检测高阶 (不相邻) 相关。此类相关在相邻误差间不存在相关时通常不出现。
Durbin-Watson 统计是 polyfitstat 返回的统计之一:
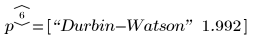
检查正态性
通过创建标准化残差的正态图来检查 Data 集是否为正态分布。
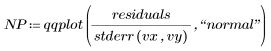
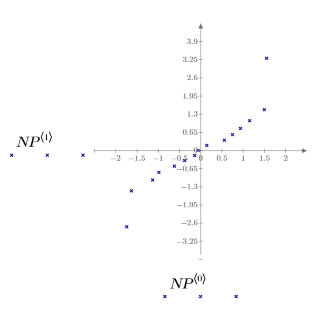
该正态图类似一条直线。因此,误差近似为正态分布。由于正态图易受其他违规假设 (例如,当误差方差不相等时) 的影响,因此最好最后检查正态性。