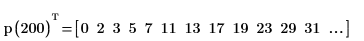示例:递归函数
使用 PTC Mathcad 编程功能来定义递归函数。
示例 1:定义阶乘函数
1. 定义函数 Fac 以计算 n 的阶乘。使用“函数”标签标记您的函数。
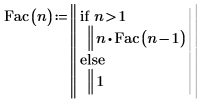
2. 使用 Fac 计算 6 的阶乘,然后使用 PTC Mathcad 阶乘运算符对其进行检查。
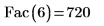
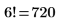
3. 使用不同的条件定义关于 n 的另一个函数 Fac,并调用该函数,如下所示。
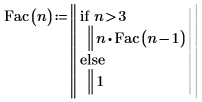
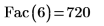
PTC Mathcad 会生成相同的结果,因为它会使用 Fac 的前一个定义来执行计算。
4. 禁用 Fac 的第一个定义来查看结果的差别。通过不重复使用函数名称来避免这种含糊不明。
示例 2:计算两个正整数的最大公约数 (GCD)
1. 写下递归函数 GCD 以计算两个数的最大公约数 (最大公约数为可整除 x 和 y 的最大整数)。
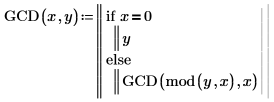
2. 使用不同值调用该函数。
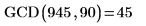 | 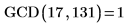 |
该程序与内置的最大公约数函数 gcd 相同:
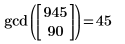 | 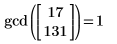 |
示例 3:定义函数 f(x) 在点 a 处的第 n 次迭代
1. 写下递归函数 nest 以计算函数 f(x) 在点 a 处的第 n 次迭代。
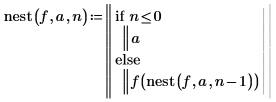
2. 定义函数 f(x) 并将 1 赋值给 a。
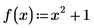
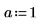
3. 使用不同值调用该函数。
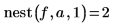 | 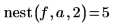 |
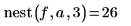 | 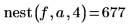 |
示例 4:定义斐波纳契序列 (每次调用两次递归调用)
1. 写下函数 fib 以计算 n 项斐波纳契序列的值。
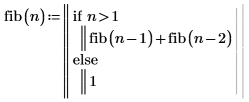
2. 定义矢量 k 并调用函数 fib。
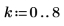

示例 5:定义分区函数
1. 写下递归函数 part 以计算将 m 表达为不超过 n 的正整数总和的不同方式数。

2. 使用不同值调用该函数。
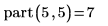
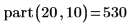
示例 6:创建随机二进制树
1. 写下创建随机二进制树的递归函数 Tree。
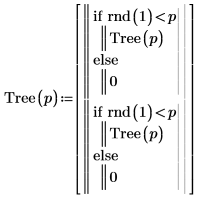
2. 调用函数。

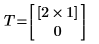
示例 7:查找二进制树的高度
1. 写下返回二进制树高度的函数 height。
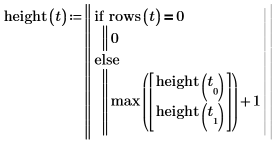
2. 使用您在先前示例中创建的树调用函数。
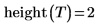
由于 Tree 创建了随机二进制树,因此,每次重新计算后返回的高度都会发生更改。 |
示例 8:设置埃拉托斯特尼筛法来查找质数

2. 调用该函数以获得一个包含所有小于 200 的质数的矢量。